Уравнение колебаний
Определение и уравнение колебаний
Колебания, происходящие по законам синуса или косинуса, называют гармоническими.
Уравнение гармонических колебаний:
![]()
где t-время; x-величина изменяющаяся со временем (координата, заряд, ток, ЭДС и т.п.); A- амплитуда колебаний – максимальное отклонение колеблющейся величины от среднего (нулевого) значения; ![]() — фаза колебаний;
— фаза колебаний; ![]() — начальная фаза; w- циклическая частота (изменение фазы в единицу времени). За период фаза меняется на
— начальная фаза; w- циклическая частота (изменение фазы в единицу времени). За период фаза меняется на ![]() .
.
![]()
Дифференциальное уравнение гармонических колебаний
Уравнение вида:
![]()
дифференциальное уравнение гармонических колебаний.
Виды периодических колебаний можно с любой степени точности можно представить в виде суммы гармонических колебаний, так называемого гармонического ряда.
Колебания, которые будет совершать тело, если его вывести из состояния равновесия (не важно как) и предоставить самому себе, называют свободными (собственными) колебаниями. Если собственные колебания вызваны наличием только квазиупругой силы, то они будут гармоническими.
Колебания тела, обусловленные одновременным действием квазиупругой силы и силы трения (которая пропорциональна мгновенной скорости: ![]() ), называют затухающими колебаниями.
), называют затухающими колебаниями.
![]()
Уравнение (3) называется дифференциальным уравнением затухающих колебаний. Здесь ![]() – коэффициент затухания.
– коэффициент затухания.
Решение дифференциального уравнения колебаний
Решением дифференциального уравнения затухающих колебаний (3) является соотношение вида:
![]()
Уравнение (4) называется уравнением затухающих колебаний. В уравнении (4) видно, что амплитуда затухающих колебаний зависит от времени. Константы A и ![]() определяются начальными условиями. Амплитуда колебаний убывает и они в целом выглядят так, как представлено на рис. 1
определяются начальными условиями. Амплитуда колебаний убывает и они в целом выглядят так, как представлено на рис. 1
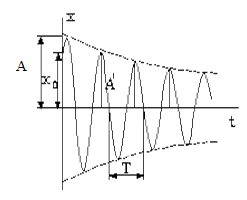
рис. 1.
Период затухающих колебаний вычисляется по формуле (5):
![]()
Физический коэффициента затухания смысл состоит в том, что коэффициент затухания – величина, обратная времени релаксации. А время релаксации – это время, за которое амплитуда уменьшается в e раз. Однако коэффициент затухания не вполне характеризует затухание. Обычно затухание колебаний характеризуется декрементом затухания. Последний показывает, во сколько раз уменьшается амплитуда колебаний за время, равное периоду колебаний. То есть декремент затухания определяется так:
![]()
Логарифм декремента затухания называется логарифмическим декрементом, он, очевидно, равен:
![]()
Если колебательная система подвергается воздействию внешней периодической силы, то возникают так называемые вынужденные колебания, имеющие незатухающий характер.
Вынужденные колебания следует отличать от автоколебаний. В случае автоколебаний в системе предполагается специальный механизм, который в такт с собственными колебаниями «поставляет» в систему небольшие порции энергии.
Примеры решения задач
| Задание |
Найдите энергию свободных колебаний груза подвешенного на пружине Рассмотрите случай физического маятника, зная, что жесткость пружины k, амплитуда колебаний A.
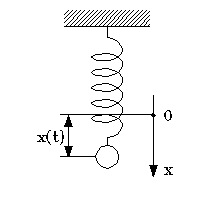
рис. 1.1 |
| Решение |
Найдем энергию свободных колебаний. Она представлена двумя видами энергии: кинетической и потенциальной. Для шарика, подвешенного на пружине:
Колебания шарика описывает уравнение колебаний: запишем уравнение колебаний скорости шарика, зная, что Подставим (1.2) и (1.3) в (1.1), получим: зная, что для физического маятника |
| Ответ | Энергия свободных колебаний пропорциональна квадрату амплитуды колебаний |
| Задание |
Одно колебательное движение осуществляется по оси Х, другое по оси Y. Колебания гармонические.
1)Частоты и фазы колебаний одинаковы, а амплитуды различны. 2) Частоты колебаний одинаковы, амплитуды различны. Фазы, складываемых колебаний отличаются друг от друга на Определите, каковы траектории результирующих движений, если эти колебания сложить? |
| Решение | Запишем уравнения колебаний для каждого движения:
Чтобы найти траекторию результирующего движения, нужно из уравнений (2.1), (2.2) исключить время. Для этого достаточно поделить почленно одно уравнение на другое, в результате чего получим: Уравнение (2.3.) показывает, что в данном случае сложение колебаний приводит к колебанию по прямой линии, тангенс угла наклона которой определяется отношением амплитуд. 2. Пусть фазы складываемых колебаний отличаются друг от друга на Чтобы найти траекторию результирующего движения, исключив время, нужно уравнения (2.3) и (2.4) возвести в квадрат, предварительно поделив их на Это — уравнение эллипса. При любых начальных фазах и любых амплитудах двух складываемых взаимно перпендикулярных колебаний одинаковой частоты результирующее колебание будет осуществляться по эллипсу. Его ориентация будет зависеть от фаз и амплитуд складываемых колебаний. |
| Ответ | 1) В этом случае сложение колебаний приводит к тому, что колебания происходят по прямой, тангенс угла наклона которой — 2) Траекторией результирующего движения является эллипс. |











