Энергия гармонических колебаний
Кинетическая и потенциальная энергия гармонических колебаний
Кинетическая энергия тела, совершающего гармонические колебания:
![]()
Потенциальная энергия тела, совершающего гармонические колебания (под действием квазиупругой силы):
![]()
Учитывая, что
![]()
можно записать:
![]()
Полная энергия гармонических колебаний
Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии:
![]()
При свободных колебаниях колебательная система получает энергию только в начальный момент времени, а далее энергия системы, а с ней и амплитуда колебаний не меняются. При движении тела кинетическая и потенциальная энергия переходят друг в друга. Когда отклонение системы от положения равновесия максимально, потенциальная энергия максимальна, а кинетическая равна нулю. При прохождении положения равновесия потенциальная энергия достигает минимума, а кинетическая энергия (а с ней и скорость, импульс тела) максимальна.
Примеры решения задач
| Задание | Материальная точка массой 10 г колеблется по закону |
| Решение | Полная энергия колеблющейся точки определяется соотношением:
Из уравнения колебаний точки амплитуда колебаний Переведем единицы в систему СИ: масса материальной точки Вычислим:
|
| Ответ | Полная энергия материальной точки |
| Задание | Амплитуда гармонических колебаний материальной точки 2 см, полная энергия колебаний 0,3 мкДж. При каком смещении |
| Решение | Запишем уравнение движения точки:
По второму закону Ньютона, сила, действующая на точку: Ускорение точки найдем, дважды продифференцировав уравнение движения: Тогда сила: откуда: Полная энергия колеблющейся точки определяется формулой: откуда и выражение для синуса перепишется в виде: Тогда смещение материальной точки: Переведем единицы в систему СИ: амплитуда колебаний Вычислим: |
| Ответ | Смещение материальной точки 1,5 см. |






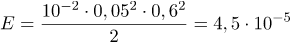 Дж
Дж




