Гармонические колебания. Уравнение гармонических колебаний
Уравнение и график гармонических колебаний
![]()
где ![]() — значение колеблющейся физической величины в момент времени
— значение колеблющейся физической величины в момент времени ![]() ;
; ![]() — амплитуда колебаний;
— амплитуда колебаний; ![]() — фаза колебаний;
— фаза колебаний; ![]() — начальная фаза.
— начальная фаза.
Графическая зависимость ![]() представляет собой синусоиду (рис.1).
представляет собой синусоиду (рис.1).
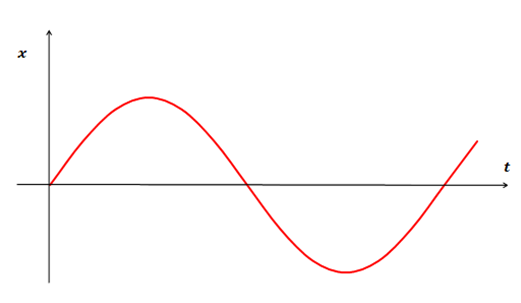
Рис.1. График гармонических колебаний
В случае механических колебаний в качестве колеблющейся величины рассматриваем смещение точки от положения равновесия.
В реальности нет таких тел, которые бы совершали гармонические колебания. Гармонические колебания – это модель, как, к примеру, моделью является материальная точка. Однако в природе есть процессы, которые хорошо описываются при помощи данной модели. Одним из таких процессов являются малые колебания груза, подвешенного на нити.
Примеры решения задач
| Задание | Написать закон изменения со временем смещения материальной точки, совершающей гармонические колебания, если амплитуда колебания 10 см, период колебания 10 с, а начальная фаза колебаний равна нулю. |
| Решение | Смещение точки, совершающей гармонические колебания, изменяется по синусоидальному закону:
Амплитуда колебаний: Закон изменения со временем смещения материальной точки: |
| Ответ | Закон изменения со временем смещения точки |
| Задание | Указать, в чем различие колебательных движений, графики которых представлены на рисунке. Определить амплитуду и период колебаний для каждого случая. Записать уравнения колебаний.
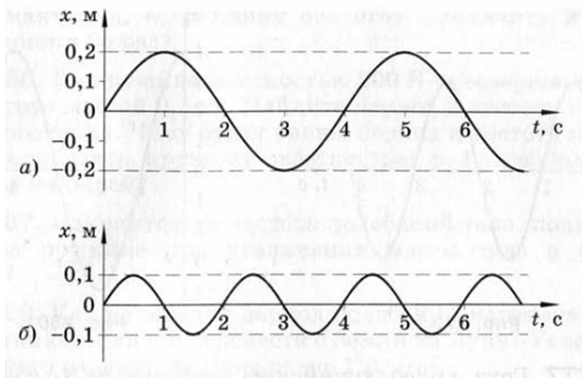
|
| Решение | Колебательные движения, представленные на графиках, отличаются амплитудами и фазами.
В случае а) амплитуда Период колебаний в случае а) Период колебаний в случае б) Начальные фазы в обоих случаях равны нулю. Уравнение гармонических колебаний в общем виде: В случае а): В случае б): |
| Ответ | Амплитуды колебаний периоды уравнения колебаний |











