Синус угла

Определение и формула синуса

ОПРЕДЕЛЕНИЕ

Синусом угла $\alpha$ острого угла прямоугольного треугольника называется отношение катета, противолежащего этому углу, к гипотенузе. Синус угла $\alpha$ обозначается $\sin \alpha .$

Рассмотрим произвольный прямоугольный треугольник $\Delta ABC,$ $\angle C={{90}^{\circ }},$ углы $\alpha$ и $\beta$ – острые. (рис. 1). Запишем, чему равны синусы острых углов $\alpha$ и $\beta .$ В рассматриваемом треугольнике $AB$ или $c$ – гипотенуза, а против угла $\alpha$ лежит катет $BC$ или $a,$ тогда

$\sin \alpha =\frac{a}{c} \quad \sin \alpha =\frac{BC}{AB}$

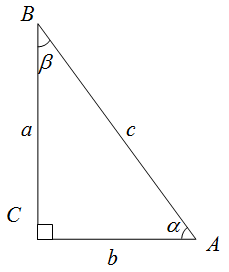
Рис. 1

Против острого угла $\beta$ лежит катет $AC$ или $b,$ тогда синус угла $\beta$ равен

$\sin \beta =\frac{b}{c} \quad \sin \beta =\frac{AC}{AB}$

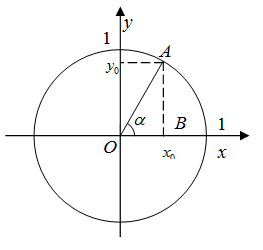
Рис. 2

Рассмотрим тригонометрический круг, то есть круг радиуса один, с центром в начале координат. Выберем произвольный угол $\alpha$ (рис. 2), которому на единичной окружности соответствует точка $A \left( {{x}_{0}},{{y}_{0}} \right).$ Опустим перпендикуляр $AB$ из точки $A$ на ось $Ox.$ Тогда $\sin \alpha =\frac{AB}{AO},$ учитывая, что радиус окружности $AO=1,$ то $\sin \alpha =AB={{y}_{0}},$ то есть синусом угла $\alpha$ есть ордината точки $A.$

Примеры решения задач

ПРИМЕР 1

Задание

Катеты прямоугольного треугольника равны соответственно 5 и $2\sqrt{6}$ см. Найти синусы острых углов треугольника.

Решение

Сделаем рисунок (рис. 3). Обозначим $a=5$ и $b=2\sqrt{6}.$ По теореме Пифагора найдем длину гипотенузы

${{c}^{2}}={{a}^{2}}+{{b}^{2}} \Rightarrow {{c}^{2}}={{5}^{2}}+{{\left( 2\sqrt{6} \right)}^{2}} \Rightarrow {{c}^{2}}=25+4\cdot 6 \Rightarrow {{c}^{2}}=49 \Rightarrow c=7 (cm)$

По определению, синус – это отношение противолежащего катета к гипотенузе, тогда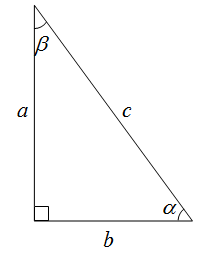

Рис. 3

$\sin \alpha =\frac{a}{c} \quad \Rightarrow \quad \sin \alpha =\frac{5}{7}$

$\sin \beta =\frac{b}{c} \quad \Rightarrow \quad \sin \beta =\frac{2\sqrt{6}}{7}$

Ответ

ПРИМЕР 2

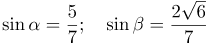Задание	Какие из точек на единичной окружности (рис. 4) удовлетворяют условию 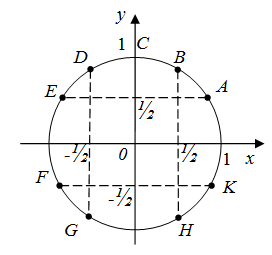$\sin \alpha =\frac{1}{2} ?$ Рис. 4
Решение	Синусом угла на окружности есть ордината конца радиуса образующего с положительным направлением оси $Ox$ заданный угол. Найдем на окружности точки, ординаты которых равны $\frac{1}{2}.$ Это точки $A$ и $E.$
Ответ	Точки A и E.

Понравился сайт? Расскажи друзьям!