Период и частота колебаний. Циклическая частота
Формулы периода и частоты колебаний
Единица измерения периода в системе СИ – секунда.
На графике колебаний период определяется как промежуток времени. через который система возвращается в то же состояние, в котором она находилась в начальный момент времени, который выбирается произвольно (рис.1).
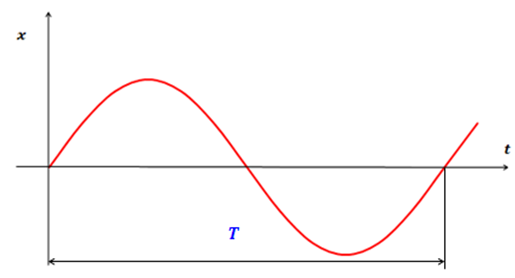
Рис.1. Определение по графику периода колебаний.
![]()
Единица измерения частоты в системе СИ – 1 Герц (Гц).
![]()
Единица измерения циклической частоты в системе СИ — рад/с.
Частота и циклическая частота связаны между собой формулой:
![]()
Примеры решения задач
| Задание | Определить частоту колебаний железнодорожных вагонов, если период их вертикального колебания равен 0,5 с. |
| Решение | Частота колебаний – это величина, обратная периоду:
|
| Ответ | Частота колебаний вагонов 2 Гц. |
| Задание | Маятник совершает 9 колебаний за 18 с. Определить период и частоту колебаний. Записать уравнение гармонических колебаний и построить график колебаний маятника, если амплитуда равна 10 см. |
| Решение | Частота колебаний определяется формулой:
Циклическая частота: Период колебаний: В общем виде уравнение гармонических колебаний: В данном случае: 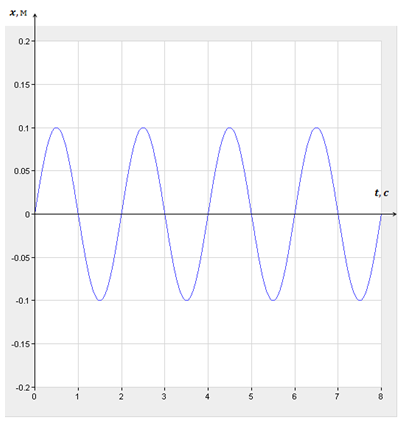
|
| Ответ | Частота колебаний 0,5 Гц; период колебаний 2 с; уравнение колебаний |
| Задание | Период колебаний крыльев шмеля 5 мс, а частота колебаний крыльев комара 600 Гц. Определить, какое насекомое и на сколько больше сделает взмахов крыльями при полете за 1 минуту. |
| Решение | Определим частоту колебаний крыльев шмеля:
С другой стороны, частота: Приравняв правые части равенств, найдем число взмахов крыльями, которое сделает шмель за время Число взмахов крыльями, которое сделает комар за время Переведем единицы в систему СИ: Вычислим: |
| Ответ | Комар сделает на 24000 взмахов крыльями больше, чем шмель. |






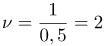 Гц
Гц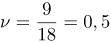 Гц
Гц




