Сложение колебаний
В природе часто происходят процессы, в которых складываются нескольких величин, изменяющихся по гармоническому закону. Это явления интерференции и дифракции света, различные акустические явления, процессы в цепях переменного тока. Сложение колебаний мы можем наблюдать на морской поверхности. Электрокардиограмма представляет собой сложение колебаний напряжений биотоков, вырабатываемых сердечной мышцей.
Метод векторных диаграмм для сложения колебаний
Для сложения колебаний удобно применять метод векторных диаграмм. Этот метод основан на представлении гармонического колебания в виде вектора, модуль которого равен амплитуде колебания, а направление образует с осью ![]() угол, равный фазе колебания (рис.1). Проекция этого вектора на ось
угол, равный фазе колебания (рис.1). Проекция этого вектора на ось ![]() равна значению
равна значению ![]() . Векторная диаграмма всегда строится для какого-то одного момента времени.
. Векторная диаграмма всегда строится для какого-то одного момента времени.
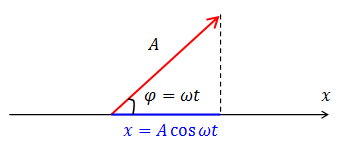
Рис.1. Представление гармонического колебания в виде вектора (метод векторных диаграмм)
Сложение колебаний одинакового направления
Рассмотрим сложение колебаний одинакового направления. Пусть складываются два гармонических колебания с различными параметрами, направленные вдоль одной прямой:
![]()
где
![]()
![]()
Пользуясь методом векторных диаграмм, представим эти колебания с помощью векторов ![]() и
и ![]() (рис.2).
(рис.2).
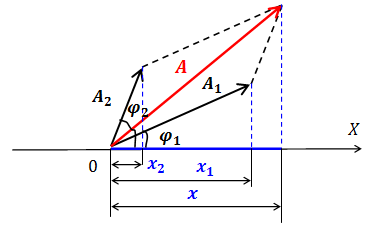
Рис.2. Сложение колебаний одинакового направления
Результирующее колебание:
![]()
Амплитуда результирующего колебания находится с использованием теоремы косинусов и равна:
![]()
Так как разность фаз в общем случае зависит от времени, то амплитуда ![]() результирующего колебания непостоянна. Поэтому результирующее колебание не является гармоническим, а представляет собой сложный колебательный процесс с пульсирующей амплитудой.
результирующего колебания непостоянна. Поэтому результирующее колебание не является гармоническим, а представляет собой сложный колебательный процесс с пульсирующей амплитудой.
Если частоты колебаний равны ![]() , то разность фаз этих колебаний не зависит от времени:
, то разность фаз этих колебаний не зависит от времени:
![]()
Такие колебания называются когерентными.
В этом случае результирующая амплитуда колебаний равна:
![]()
а начальная фаза результирующего колебания определяется соотношением:
![]()
Очевидно, что:
- если разность начальных фаз обоих колебаний
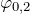 —
— 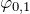 равна 0 или
равна 0 или 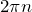 , то
, то 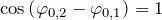 и амплитуда результирующего колебания максимальна и равна сумме амплитуд складываемых колебаний:
и амплитуда результирующего колебания максимальна и равна сумме амплитуд складываемых колебаний: 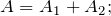
- если разность начальных фаз равна
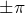 , т.е.
, т.е. 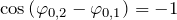 (колебания находятся в противофазе), амплитуда результирующего колебания минимальна и равна:
(колебания находятся в противофазе), амплитуда результирующего колебания минимальна и равна: 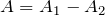 , в случае равенства амплитуд
, в случае равенства амплитуд 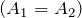 наблюдается полное гашение колебаний.
наблюдается полное гашение колебаний.
Примеры решения задач
| Задание | Два одинаково направленных колебания с равными частотами имеют амплитуды 20 и 50 см. Второе колебание опережает первое по фазе на |
| Решение | При сложении и двух колебаний с одинаковыми частотами, происходящих в одном направлении, амплитуда результирующего колебания:
Переведем в систему СИ значения амплитуд: Вычислим: Начальная фаза суммарного колебания: |
| Ответ | Амплитуда суммарного колебания 68 см, начальная фаза суммарного колебания |
| Задание | Складываются два одинаково направленных колебания |
| Решение | Воспользуемся тригонометрической формулой приведения:
и перепишем уравнение первого колебания в виде: Построим векторную диаграмму для момента времени 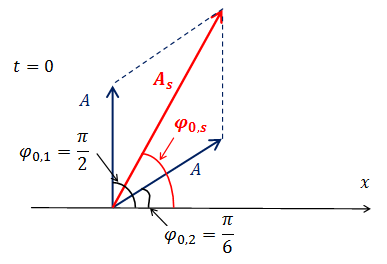
Амплитуда суммарного колебания определяется формулой: В данном случае: Начальная фаза суммарного колебания: Поэтому: Уравнение результирующих колебаний: |
| Ответ | Амплитуда результирующего колебания начальная фаза результирующего колебания уравнение результирующих колебаний |











