Теорема косинусов
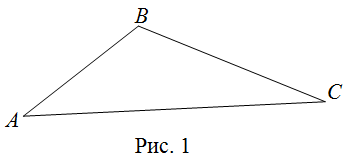
То есть для треугольника ![]() , изображенного на рисунке 1, имеют место следующие соотношения:
, изображенного на рисунке 1, имеют место следующие соотношения:
![]()
![]()
![]()
Следствие из теоремы косинусов
Косинус любого угла треугольника ![]() , при условии, что известны все его стороны, можно найти из соотношений
, при условии, что известны все его стороны, можно найти из соотношений
![]()
![]()
![]()
Примеры решения задач
| Задание | В треугольнике |
| Решение | Запишем для неизвестной стороны Подставляя известные значения сторон и угла, получим:
|
| Ответ |
| Задание | Стороны треугольника равны соответственно 3, 7 и 8 см. Найти угол, лежащий против стороны длинной 7 см. |
| Решение | Обозначим стороны треугольника: Подставим известные значения длин сторон, получим |
| Ответ |











