Теорема синусов

ТЕОРЕМА

В произвольном треугольнике стороны пропорциональны синусам противоположных углов (рис. 1):

$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$

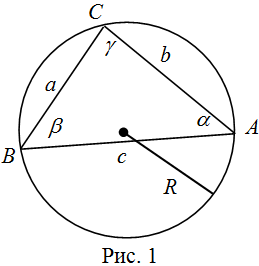
Доказательство теоремы

Рассмотрим произвольный треугольник $ABC$ (рис. 1). Запишем для него формулу площади через две стороны и угол между ними:

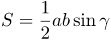или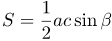

Приравнивая правые части этих формул, получим

$\frac{1}{2} ab \sin \gamma = \frac{1}{2}ac \sin \beta$

сократим левую и правую часть этого равенства на $\frac{1}{2}a$ ,

$b \sin \gamma = c \sin \beta \text{ } \Rightarrow \text{ } \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$

Аналогично, из формулы

$S = \frac{1}{2} bc \sin \alpha$

выводится равенство

$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}$

Приравнивая (1) и (2), получим

$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$

Теорема доказана.

Расширенная теорема синусов

ТЕОРЕМА

В произвольном треугольнике отношение стороны треугольника к синусу противоположного угла равно диаметру описанной около него окружности (рис. 1):

$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = 2 R$

Примеры решения задач

ПРИМЕР 1

Задание

Одна из сторон треугольника равна 6 см, противолежащий угол равен $60 ^\circ$ , а один из прилежащих $45 ^\circ$ . Найти длину стороны, лежащей против угла в $45 ^\circ$ .

Решение

Воспользуемся рисунком 1 и введем следующие обозначения. Сторона $a=6$ см, $\angle \alpha = 60 ^\circ$ , $\angle \beta = 45 ^\circ$ , $b$ – неизвестная сторона. Запишем для этих сторон и углов теорему синусов:

$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}$

Выразим из последнего равенства неизвестную сторону $b$ :

$b = \frac{6 \cdot \sin \beta}{\sin \alpha}$