Теорема о трех перпендикулярах
ТЕОРЕМА
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
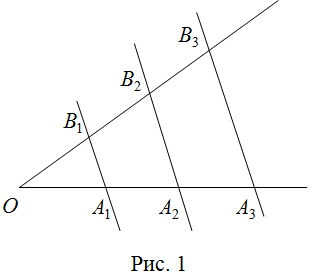
На рисунке 1, по теореме Фалеса, если прямые ![]() , а отрезки
, а отрезки ![]() , то
, то ![]() .
.
Обобщение теоремы Фалеса (Теорема о пропорциональных отрезках)
ТЕОРЕМА
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
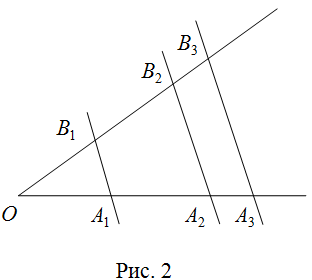
На рисунке 2, согласно обобщенной теореме Фалеса, если ![]() , то
, то
![]()
Примеры решения задач
ПРИМЕР 1
| Задание | На рисунке 3, 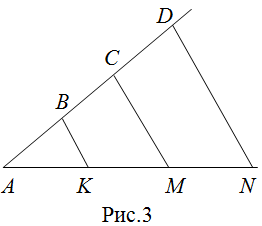
|
| Решение | По теореме Фалеса, так как |
| Ответ |
ПРИМЕР 2
| Задание | В треугольнике |
| Решение | Сделаем рисунок (рис. 4).
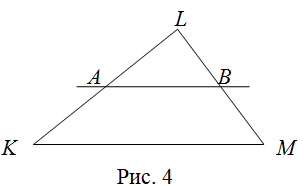
Так как
По теореме Фалеса, так как Что и требовалось доказать. |











