Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Теоремы Теорема Пифагора

Теорема Пифагора

ТЕОРЕМА

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

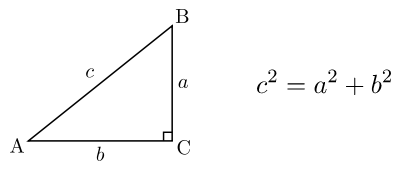
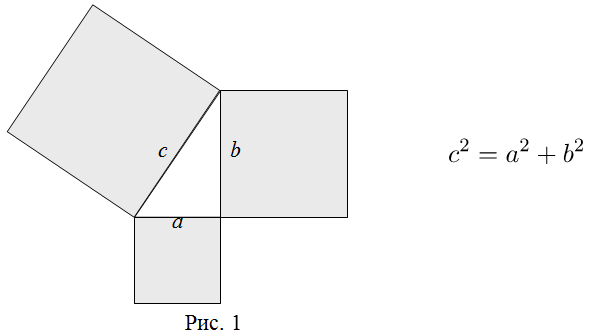
Геометрическая формулировка теоремы Пифагора

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (рис. 1).

Доказательство теоремы Пифагора

Площадь прямоугольного треугольника вычисляется по формуле

$S = \frac{1}{2} ab$

С другой стороны для вычисления площади произвольного треугольника справедлива формула: $S =pr$ . В этой формуле $p$ – полупериметр $p=\frac{1}{2}(a+b+c)$ , а $r$ – радиус вписанной окружности и для прямоугольника он равен $r=\frac{1}{2}(a+b-c)$ . Далее приравнивая правые части обеих формул для площади треугольника, получим

$\frac{1}{2} ab = \frac{1}{2}(a+b+c) \frac{1}{2}(a+b-c)$

$2 ab = (a+b+c) (a+b-c)$

$2 ab = \left( (a+b)^{2} -c^{2} \right)$

$2 ab = a^{2}+2ab+b^{2}-c^{2}$

$0=a^{2}+b^{2}-c^{2}$

$c^{2} = a^{2}+b^{2}$

Что и требовалось доказать.

Примеры решения задач

ПРИМЕР 1

Задание

Катеты прямоугольного треугольника равны 12 см и 5 см. Найти гипотенузу.

Решение

Обозначим катеты $a=12$ см и $b=5$ см, а гипотенузу – $c$ . По теореме Пифагора гипотенуза будет равна

$c^{2} = a^{2} + b^{2}$

Подставляя длины катетов, получим

$c^{2}=12^{2}+5^{2} \text{ } \Rightarrow \text{ } c^{2}=169 \text{ } \Rightarrow \text{ } c = \sqrt{169} \text{ } \Rightarrow \text{ } c = 13$ (см)

Ответ

Гипотенуза прямоугольного треугольника равна 13 см

ПРИМЕР 2

Задание

Диагональ прямоугольника $ABCD$ равна 5 см, а одна из его сторон – 3 см. Найти вторую сторону прямоугольника.

Решение

Сделаем рисунок (рис. 2).

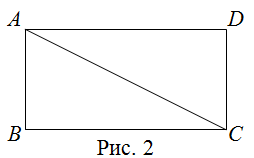
Обозначим $AC=5$ см, $AB=3$ см. Рассмотрим прямоугольный треугольник $ABC$ . Запишем для него теорему Пифагора:

$AC^{2} = AB^{2} + BC^{2}$

Выразим из последнего равенства неизвестную сторону $BC$ :

$BC = \sqrt{AC^{2}-AB^{2}}$

Подставляя известные значения сторон, получим

$BC = \sqrt{5^{2}-3^{2}}$

$BC = \sqrt{25-9}$

$BC = \sqrt{16}$

$BC=4$ (см)

Ответ

Вторая сторона прямоугольника равна 4 см

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook