Прямоугольный треугольник
Определение и формулы прямоугольного треугольника
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
Для прямоугольного треугольника справедливы следующие утверждения:
- Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
- Сумма острых углов прямоугольного треугольника равна
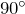 :
: - Гипотенуза прямоугольного треугольника больше каждого их катетов:
- Катет, лежащий против угла
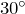 , равен половине гипотенузы.
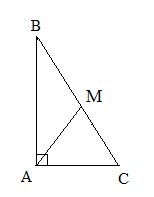
, равен половине гипотенузы. - Две высоты прямоугольного треугольника совпадают с его катетами.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
- Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:
![]()
![]()
![]()
![]()
Признаки равенства прямоугольных треугольников
- По двум катетам: если два катета одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
- По стороне и острому углу: Если сторона и прилежащий к ней острый угол одного прямоугольного треугольника соответственно равны стороне и прилежащему к ней острому углу другого прямоугольного треугольника, то такие треугольники равны
Подробнее про признаки равенства треугольников читайте по ссылке.
Тригонометрические соотношения в прямоугольном треугольнике
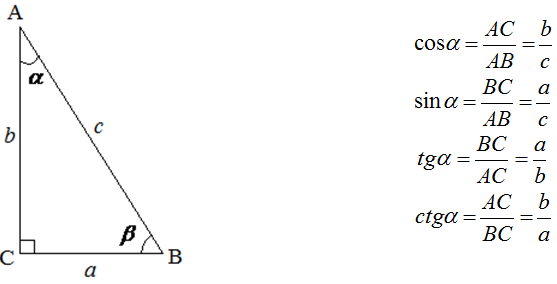
Площадь прямоугольного треугольника равна половине произведения катетов и вычисляется по формуле
![]()
Примеры решения задач
| Задание | В прямоугольном треугольнике |
| Решение | В прямоугольном треугольнике сумма острых углов равна 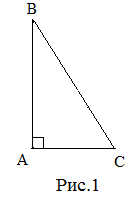
Также известно, что катет
|
| Ответ |
| Задание | В равнобедренном треугольнике |
| Решение | Запишем для прямоугольного треугольника Так как этот треугольник равнобедренный, то откуда Площадь прямоугольного треугольника равна половине произведения катетов, т.е. |
| Ответ |











