Признаки равенства треугольников

Три признака равенства треугольников

I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

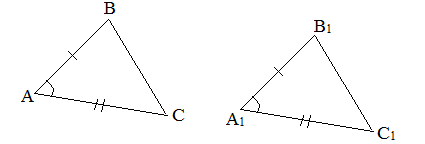
II признак (по стороне и прилежащим углам) Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

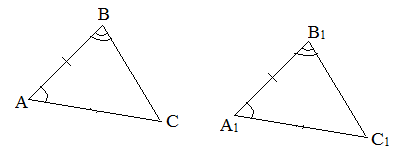
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

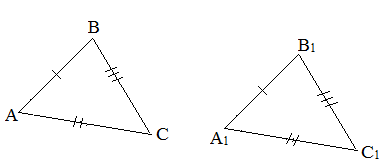
Примеры решения задач

ПРИМЕР 1

Задание

Известно, что в четырехугольнике 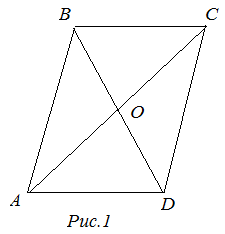$ABCD$ стороны $AB=CD$ и $AB||CD$ (рис.1). Доказать, что треугольники $AOB$ и $COD$ равны.

Доказательство

В четырехугольнике $ABCD$ проведем диагонали $AC$ и $BD$ , которые пересекаются в точке $O$ . Рассмотрим треугольники $AOB$ и $COD$ . Поскольку $AB||CD$ , а $AC$ и $BD$ – секущие, то $\angle OBA=\angle ODC$ и $\angle OAB=\angle OCD$ (как внутренние накрест лежащие углы). Также, по условию, $AB=CD$ , поэтому треугольники $AOB$ и $COD$ равны между собой (по второму признаку равенства треугольников)

Что и требовалось доказать.

ПРИМЕР 2

Задание	Вычислить площадь равнобедренного треугольника 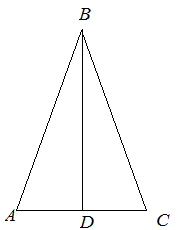$ABC$ , если на основании $AC$ отмечена точка $D$ так, что $AD=CD$ , а площадь треугольника $ADC$ равен $15$ см $^{2}$ .
Решение	В треугольнике $ABC$ проведем отрезок $BD$ так, что $AD=CD$ . По условию $AB=BC$ и $\angle A=\angle C$ (т.к. $ABC$ – равнобедренный), а значит треугольники $ABD$ и $CBD$ – равны (по первому признаку равенства треугольников). Следовательно, $S_{ABC} =2S_{ABD} =2\cdot 15=30$ см $^{2}$
Ответ	$S_{ABC} =30$ см $^{2}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Признаки равенства треугольников

Три признака равенства треугольников

Примеры решения задач