Свойства прямоугольного треугольника
ОПРЕДЕЛЕНИЕ
Треугольник называется прямоугольным, если один из его углов прямой, то есть равен 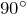 . Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла – гипотенуза.
. Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла – гипотенуза.
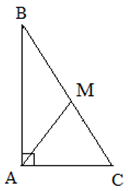
Свойства прямоугольного треугольника:
- Сумма острых углов треугольника равна
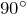 :
:
![Rendered by QuickLaTeX.com \[\angle B+\angle C={{90}^{\circ}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ebca932ae7124f9e6d4f701a5fb0eeed_l3.png)
- Гипотенуза прямоугольного треугольника больше каждого их катетов:
![Rendered by QuickLaTeX.com \[AC<BC, \quad AB<BC\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3ef1e0d9a6e3ee4069c7d5be508ed3b4_l3.png)
- Катет, лежащий против угла 30о, равен половине гипотенузы.
- Две высоты прямоугольного треугольника совпадают с его катетами.
- Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
- Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:
![Rendered by QuickLaTeX.com \[AM=R\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3e5dbcfaeacd4cfd16c422c46fcd02ed_l3.png)
- Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
![Rendered by QuickLaTeX.com \[A{{C}^{2}}+A{{B}^{2}}=B{{C}^{2}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2a64260dd02aadc4e445fb99c95f6e13_l3.png)
Примеры решения задач
ПРИМЕР 1
| Задание | В прямоугольном треугольнике 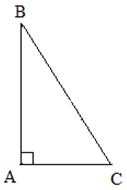
|
| Решение | В прямоугольном треугольнике сумма острых углов равна Также известно, что катет, лежащий против угла |
| Ответ |
ПРИМЕР 2
| Задание | В треугольнике |
| Решение | Треугольнике Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы, следовательно, |
| Ответ |











