Треугольник

Определение треугольника

ОПРЕДЕЛЕНИЕ

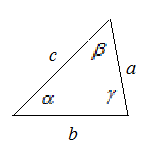
Треугольник это геометрическая фигура, состоящая из трех точек и трех отрезков, попарно их соединяющих.

В любом треугольнике три угла и три стороны.

ТЕОРЕМА

Сумма углов любого треугольника равна $180^{\circ}$ .

Против большего угла треугольника лежит большая сторона.

Виды треугольников

Треугольники бывают

остроугольными (если все его углы острые),
тупоугольными (если один из его углов тупой),
прямоугольными (если один из его углов прямой).

Треугольник называется

равнобедренным, если две его стороны равны.
равносторонним, если все три стороны равны,
разносторонним, если все его стороны разные.

Основные линии треугольника

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.

Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).

Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.

В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.

Признаки равенства треугольников

I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

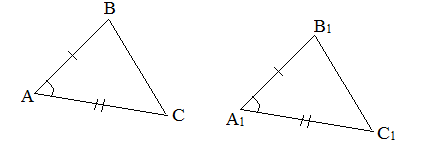
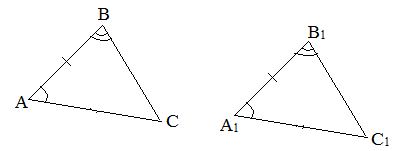
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

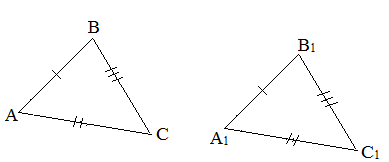
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Подробнее про признаки равенства треугольников читайте по ссылке.

Признаки подобия треугольников

Треугольники называются подобными, если их стороны пропорциональны.

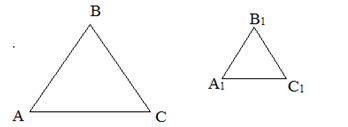
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.

II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.

III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Подробнее про признаки подобия треугольников читайте по ссылке.

Теоремы треугольников

Для любого треугольника справедливы следующие теоремы.

ТЕОРЕМА

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

$c^{2} =a^{2} +b^{2} -2ab\cos (\widehat{a;b})$

Подробнее про теорему косинусов читайте по ссылке.

ТЕОРЕМА

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной вокруг этого треугольника окружности:

$\frac{a}{\sin \alpha } =\frac{b}{\sin \beta } =\frac{c}{\sin \gamma } =2R$

Подробнее про теорему синусов читайте по ссылке.

Примеры решения задач

ПРИМЕР 1

Задание

Доказать, что в равнобокой трапеции диагонали равны.

Доказательство

В равнобокой трапеции 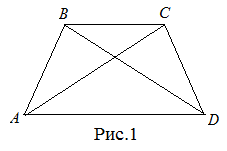$ABCD$ рассмотрим треугольники $ABD$ и $ACD$ (рис. 1). Так как $AB=CD, \angle BAD=\angle CDA, AD$ – общая сторона, то треугольники $ABD$ и $ACD$ равны по первому признаку, а значит, равны все их элементы, т.е. $AC=BD$ .

Что и требовалось доказать.

ПРИМЕР 2

Задание

В треугольнике $ABC$ стороны $AB=8$ см $, BC=12$ см $, AC=16$ см. На стороне $AC$ отмечена точка $D$ так, чтобы $CD=9$ см. Найти отрезок $BD$ .

Решение

Рассмотрим треугольники 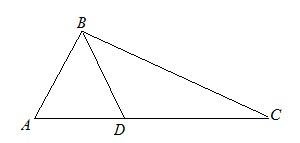$ABC$ и $BDC$ . Запишем отношение сторон $BC:DC$ и $AC:BC$ :

$12:9=16:12$

Так как выполняется равенство отношений, то соответствующие стороны треугольников пропорциональны, а также $\angle C$ – общий угол. Следовательно, треугольники $ABC$ и $BDC$ – подобны (по второму признаку подобия). Найдем сторону $BD$ :

$AB:BD=BC:DC,\ 8:BD=12:9,\$

откуда $BD=6$ см.

Ответ

$BD=6$ см.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Треугольник

Определение треугольника

Виды треугольников

Основные линии треугольника

Признаки равенства треугольников

Признаки подобия треугольников

Теоремы треугольников

Примеры решения задач