Второй признак подобия треугольников

ОПРЕДЕЛЕНИЕ

Второй признак подобия треугольников (по двум сторонам и углу): если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.

Примеры решения задач

ПРИМЕР 1

Задание

На одной стороне угла $A$ отложены отрезки $AB$ и $AD$ , а на другой – $AC$ и $AE$ . Подобны ли треугольники $ABC$ и $ADE$ , если $AB=4$ см $,\ AD=20$ см $,\ AC=10$ см и $AE=8$ см.

Решение

Рассмотрим треугольники 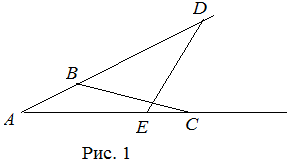$ABC$ и $ADE$ , у которых угол $A$ – общий. Запишем отношения соответствующих сторон

$\frac{AB}{AE} =\frac{4}{8} =\frac{1}{2}$

$\frac{AC}{AD} =\frac{10}{20} =\frac{1}{2}$

Получили, что две стороны одного треугольника пропорциональны двум сторонам другого треугольника и при этом треугольники имеют общий угол, а значит, эти треугольники подобны (по второму признаку подобия).

Ответ

Треугольники $ABC$ и $ADE$ подобны.

ПРИМЕР 2

Задание	На сторонах 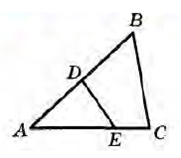$AB$ и $AC$ треугольника $ABC$ отметили соответственно точки $D$ и $E$ так, что $AD=\frac{4}{7} AC,\ AE=\frac{4}{7} AB$ . Найти $DE$ , если $BC=21$ см.
Решение	Треугольники $ABC$ и $AED$ имеют общий угол $A$ и две пары пропорциональных сторон. Значит, эти треугольники подобны (по второму признаку подобия) с коэффициентом подобия $\frac{4}{7}$ . Из этого следует, что $DE=\frac{4}{7} \cdot BC=\frac{4}{7} \cdot 21=12\ cm$
Ответ	$DE=12$ см

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Второй признак подобия треугольников

Примеры решения задач