Остроугольный треугольник

Определение остроугольного треугольника

ОПРЕДЕЛЕНИЕ

Остроугольным треугольником называется треугольник, у которого все углы острые (т.е. меньше 90 градусов).

В остроугольном треугольнике медиана, проведённая из любой вершины, больше половины стороны, на которую она опущена.

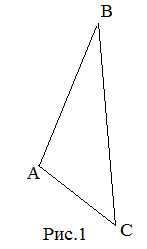
Примеры решения задач

ПРИМЕР 1

Задание

Выяснить, является ли треугольник остроугольным, если его стороны равны $a=5$ см $, b=4$ см и $c=4$ см.

Решение

Поскольку в треугольнике против большего угла лежит большая сторона, то запишем теорему косинусов для стороны $a$ :

$a^{2} =b^{2} +c^{2} -2bc\cos \alpha ,$

$25=16+16-2\cdot 4\cdot 4\cdot \cos \alpha ,$

откуда $\cos \alpha =\frac{7}{32} =0,2188$ . Из таблиц Брадиса узнаем какому углу соответствует это значение косинуса. Это угол $\alpha =77^{\circ} 22'$ . Получаем, что больший угол треугольника острый, а значит треугольник остроугольный.

Ответ

Треугольник остроугольный.

ПРИМЕР 2

Задание

В остроугольном треугольнике $ABC$ высоты $AK$ и $BH$ пересекаются в точке $E$ . Доказать, что углы $AKH$ и $ABH$ равны.

Доказательство

Рассмотрим прямоугольные треугольники 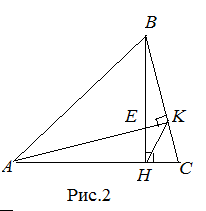$AEH$ и $BEK$ (рисунок 2), $\angle AEH=\angle BEK$ (как вертикальные). Следовательно, треугольники подобны, откуда

$\frac{EH}{EK} =\frac{AE}{EB}$

Далее рассмотрим треугольники $EHK$ и $AEB$ , в которых $\angle AEB=HEK$ (как вертикальные) и $\frac{EH}{AE} =\frac{EK}{EB}$ . Следовательно, треугольники подобны, а значит $AKH=ABH$ .

Что и требовалось доказать.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Остроугольный треугольник

Определение остроугольного треугольника

Примеры решения задач