Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Окружность, описанная около треугольника

Окружность, описанная около треугольника

Определение и формулы окружности, описанной около треугольник

ОПРЕДЕЛЕНИЕ

Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью.

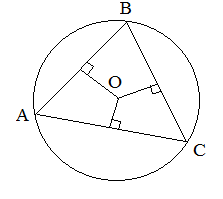
Окружность, описанная около треугольника

Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Вокруг любого треугольника можно описать окружность, причем только одну.
Радиус 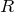$R$ окружности, описанной около треугольника, равен отношению произведения сторон 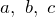$a,\ b,\ c$ треугольника к его учетверенной площади:

$R=\frac{abc}{4S}$

Радиус окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла (следствие теоремы синусов):

$R=\frac{AB}{2\sin \angle C} =\frac{AC}{2\sin \angle B} =\frac{BC}{2\sin \angle A}$

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.

Примеры решения задач

ПРИМЕР 1

Задание

Найти радиус окружности, описанной около треугольника $ABC$ со стороной $AB=3$ см и углами $\angle A=60^{\circ}$ и $\angle B =75^{\circ}$

Решение

Радиус $R$ окружности, описанной около треугольника, найдем из равенства

$R=\frac{AB}{2\sin \angle C}$

Сумма углов произвольного треугольника равна 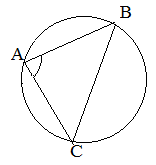$180^{\circ}$ , поэтому

$\angle C=180^{\circ} -60^{\circ} -75^{\circ} =45^{\circ}$

Теперь можно найти радиус описанной окружности:

$R=\frac{3}{2\cdot \frac{\sqrt{2} }{2} } =\frac{3}{\sqrt{2} } =\frac{3\sqrt{2} }{2} \ cm$

Ответ

$R=\frac{3\sqrt{2} }{2}$ см.

ПРИМЕР 2

Задание

В треугольнике $ABC$ стороны $AB=8$ см $, AC=4$ см. Найти все углы треугольника, если радиус описанной окружности равен $R=4$ см.

Решение

Радиус описанной окружности равен отношению стороны треугольника к удвоенному синусу противолежащего угла

$R=\frac{AB}{2\sin \angle C} =\frac{AC}{2\sin \angle B} =\frac{BC}{2\sin \angle A}$

Из записанных равенств найдем синусы углов В и С треугольника:

$\sin \angle C=\frac{AB}{2R} =\frac{8}{8} =1,\ \sin \angle B=\frac{AC}{2R} =\frac{6}{8} =\frac{1}{2} ,$

откуда следует, что $\angle C=90^{\circ}$ , а $\angle B=30^{\circ}$

Найдем величину угла $A$ :

$\angle A=180^{\circ} -90^{\circ} -30^{\circ} =60^{\circ}$

Ответ

$\angle A=60^{\circ} , \angle B=30^{\circ} , \angle C=90^{\circ}$ .

Читайте также:

Формулы треугольника

Египетский треугольник

Неравенство треугольника

Виды треугольников

Тупоугольный треугольник

Остроугольный треугольник

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook