Теорема о сумме углов треугольника
Доказательство теоремы о сумме углов треугольника
Рассмотрим треугольник ![]() (рис. 1).
(рис. 1).
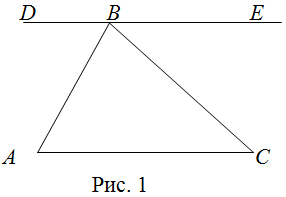
Через вершину ![]() проведем прямую
проведем прямую ![]() параллельно основанию
параллельно основанию ![]() . Тогда
. Тогда ![]() как внутренние накрест лежащие при параллельных
как внутренние накрест лежащие при параллельных ![]() и
и ![]() , и секущей
, и секущей ![]() . Аналогично,
. Аналогично, ![]() внутренние накрест лежащие при
внутренние накрест лежащие при ![]() и секущей
и секущей ![]() . Угол
. Угол ![]() развернутый и равен
развернутый и равен
![]()
Учитывая, что развернутый угол равен ![]() , а
, а ![]() и
и ![]() , окончательно получим
, окончательно получим
![]()
Теорема доказана.
Примеры решения задач
| Задание | Угол при основании равнобедренного треугольника равен |
| Решение | Сделаем рисунок (рис. 2).
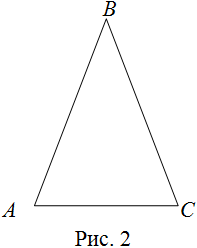
По условию, треугольник По теореме о сумме углов треугольника Выразим из последнего равенства Подставляя заданные значения углов |
| Ответ |
| Задание | Найти углы треугольника |
| Решение | Сложим, левые и правые части заданных равенств По теореме о сумме углов треугольника Тогда |
| Ответ |











