Формулы треугольника
Формулы площади треугольника
1. По стороне и проведенной к ней высоте
![]()
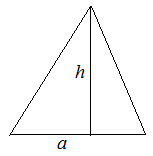
2. По двум сторонам и углу между ними
![]()
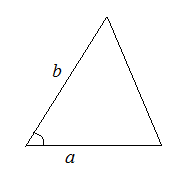
![]()
где ![]() – полупериметр треугольника
– полупериметр треугольника
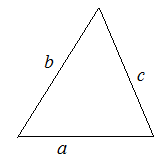
4. Через радиусы вписанной и описанной окружностей
![]()
где ![]() – полупериметр треугольника,
– полупериметр треугольника, ![]() – радиус вписанной окружности;
– радиус вписанной окружности;
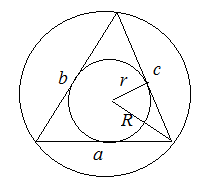
![]()
здесь ![]() – радиус описанной окружности.
– радиус описанной окружности.
Теоремы треугольника
![]()
![]()
![Rendered by QuickLaTeX.com \[\frac{a-b}{a+b} =\frac{\text{tg}\frac{\alpha -\beta }{2} }{\text{tg}\frac{\alpha +\beta }{2} } \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-879930b308cf91d140e0f0466a3eb415_l3.png)
Равносторонний треугольник со стороной ![]() :
:
![]() – радиус описанной окружности,
– радиус описанной окружности,
![]() – радиус вписанной окружности,
– радиус вписанной окружности,
![]() – высота, совпадающая с медианой и биссектрисой,
– высота, совпадающая с медианой и биссектрисой,
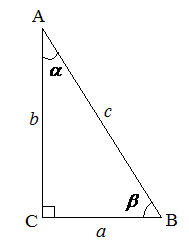
Формулы прямоугольного треугольника
В прямоугольном треугольнике ![]() с
с ![]() , гипотенузой
, гипотенузой ![]() и катетами
и катетами ![]() и
и ![]()
![]()
![]()
![]()
Примеры решения задач
| Задание | В равностороннем треугольнике со стороной |
| Решение | Площадь равностороннего треугольника найдем по формуле Тогда искомые радиусы вписанной и описанной окружностей |
| Ответ |
| Задание | В треугольнике |
| Решение | Сделаем рисунок.
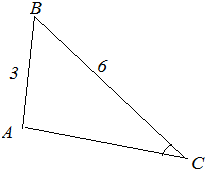
откуда Найдем сторону
|
| Ответ |











