Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Окружность, вписанная в прямоугольный треугольник

Окружность, вписанная в прямоугольный треугольник

Определение и формулы вписанной окружности

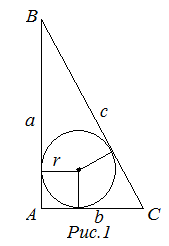
Рассмотрим прямоугольный треугольник $ABC$ с катетами $a,b$ и гипотенузой $c$ (рис. 1). Тогда радиус $r$ вписанной в этот треугольник окружности будет равен

$r=\frac{a+b-c}{2}$

Окружность, вписанная в прямоугольный треугольник

Примеры решения задач

ПРИМЕР 1

Задание

Найти радиус вписанной окружности прямоугольного треугольника $ABC$ со сторонами $AB=8$ см и $BC=10$ см.

Решение

В треугольнике $ABC$ (рис. 1) известны катет $AB$ и гипотенуза $BC$ , найдем второй катет $AC$ (по теореме Пифагора):

$AC=\sqrt{BC^2 -AB^2 } =\sqrt{100-64} =\sqrt{36} =6$ см

Теперь можем найти радиус вписанной окружности:

$r=\frac{AB+AC-BC}{2} =\frac{8+6-10}{2} =2\ cm$

Ответ

$r=2$ см

ПРИМЕР 2

Задание

Найти площадь равнобедренного прямоугольного треугольника $ABC$ с гипотенузой $BC=8$ см и радиусом вписанной окружности $r=3$ см.

Решение

Обозначим катеты $AB=AC$ треугольника $ABC$ через $x$ . Воспользуемся формулой для радиуса вписанной окружности прямоугольного треугольника

$r=\frac{AB+AC-BC}{2}$

$3=\frac{x+x-8}{2}$

откуда $x=7$ , т.е.

$AB=AC=7$ см

Тогда площадь треугольника $ABC$ :

$S=\frac{1}{2} \cdot AB\cdot AC=\frac{1}{2} \cdot 7\cdot 7=24,5\ cm^2$

Ответ

$S=24,5$ см $^{2}$

Читайте также:

Радиус описанной окружности около треугольника

Центр окружности вписанной в треугольник

Углы в прямоугольном треугольнике

Стороны прямоугольного треугольника

Равенство треугольников

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook