Гипотенуза прямоугольного треугольника

Определение и формула гипотенузы прямоугольного треугольника

ОПРЕДЕЛЕНИЕ

Гипотенузой прямоугольного треугольника называется сторона, лежащая против прямого угла рассматриваемого треугольника.

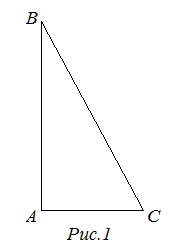
Стороны, образующие прямой угол, называются катетами.

На рисунке 1 изображен прямоугольный треугольник $ABC$ с гипотенузой $BC$ и катетами $AB$ и $AC$ .

Для гипотенузы прямоугольного треугольника можно сформулировать следующие утверждения:

Гипотенуза прямоугольного треугольника больше каждого их катетов: $BC>AC,\ BC>AB$ .
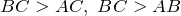Катет, лежащий против угла 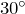$30^{\circ}$ , равен половине гипотенузы.
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора):

$AC^2 +AB^2 =BC^2$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном равнобедренном треугольнике гипотенуза больше катета на $2$ см. Найти гипотенузу.

Решение

Рассмотрим равнобедренный прямоугольный треугольник $ABC$ . Пусть катеты $AB=AC=x$ , тогда $BC=x+2$ . Пользуясь теоремой Пифагора составим уравнение

$x^2 +x^2 =(x+2)^2$ или $x^2 -4x-4=0$ .

Корнями данного квадратного уравнения будут $x_1 =2+2\sqrt{2}$ и $x_2 =2-2\sqrt{2}$ . Второй корень не подходит по смыслу задачи (поскольку является отрицательным числом), поэтому

$AB=AC=(2+2\sqrt{2} )$ см,

а гипотенуза

$BC=(4+2\sqrt{2} )$ см

Ответ

$BC=(4+2\sqrt{2} )$ см

ПРИМЕР 2

Задание

Вокруг прямоугольного треугольника описана окружность радиуса 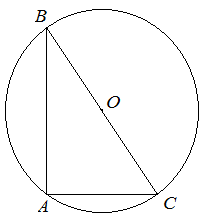$r=5$ см, а один из катетов треугольника равен $8$ см. Найти площадь треугольника.

Решение

Рассмотрим прямоугольник $ABC$ с катетом $AB=8$ см, вокруг которого описана окружность. Поскольку радиус описанной окружности лежит на середине гипотенузы, то

$OB=OC=5$ см