Виды треугольников
Определение и виды треугольников
Треугольники можно классифицировать следующим образом:
- по углам:
– тупоугольные (если один из углов треугольника тупой),
– остроугольные (если все углы треугольника острые),
– прямоугольные (если один из углов треугольника прямой)
- по сторонам:
– равнобедренные (если две стороны равны),
– равносторонние (если все стороны равны),
– разносторонние (если все стороны разные).
Примеры решения задач
| Задание | В прямоугольном равнобедренном треугольнике гипотенуза равна |
| Решение | Сделаем рисунок.
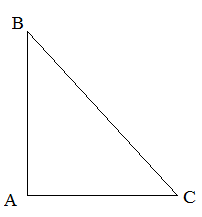
откуда
|
| Ответ |
| Задание | В треугольнике |
| Решение |
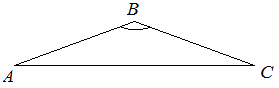
Подставляя известные данные, будем иметь: откуда Так как
|
| Ответ |











