Центр окружности описанной около треугольника

ОПРЕДЕЛЕНИЕ

Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью.

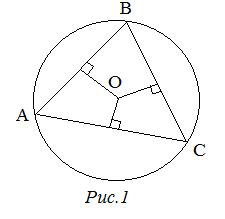
Центр окружности, описанной около треугольника

Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

В прямоугольном треугольнике центр описанной окружности находится на середине гипотенузы.

Примеры решения задач

ПРИМЕР 1

Задание

Доказать, что в треугольнике 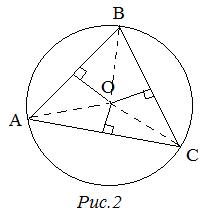$ABC$ точка пересечения серединных перпендикуляров является центром описанной окружности.

Доказательство

Пусть серединные перпендикуляры к сторонам $AB,\ BC$ и $AC$ пересекаются в точке $O$ . Соединим точку $O$ с вершинами треугольника. Поскольку точка $O$ лежит на серединных перпендикулярах, то справедливы равенства

$OA=OC,\ OC=OB,\ OB=OA$

Поэтому окружность с центром $O$ радиуса $OA$ проходит через все три вершины треугольника а, значит, является описанной около треугольника $ABC$ .

Что и требовалось доказать.

ПРИМЕР 2

Задание

В прямоугольном треугольнике 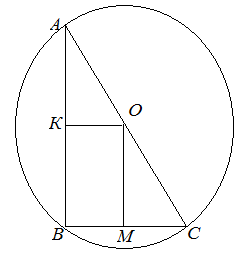$ABC$ с $\angle A=30^{\circ}$ найти расстояние от центра описанной окружности до середин катетов, если радиус описанной окружности равен $R=5$ см.

Решение

Рассмотрим треугольник $ABC$ с прямым углом $B$ . Отметим на серединах катетов $AB$ и $BC$ точки $K$ и $M$ соответственно. Поскольку центр описанной окружности прямоугольного треугольника находится на середине гипотенузы, то отрезки $OK$ и $OM$ являются средними линиями треугольника $ABC$ . Так как $R=5$ см, то гипотенуза

$AC=2R=10$ см