Радиус описанной окружности около треугольника

Определение и формула радиуса описанной окружности

ОПРЕДЕЛЕНИЕ

Окружность, проходящая через все три вершины треугольника, называется описанной вокруг этого треугольника окружностью.

Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Радиус $R$ окружности, описанной около треугольника, равен отношению произведения сторон a, b, c треугольника к его учетверенной площади:

$R=\frac{abc}{4S}$

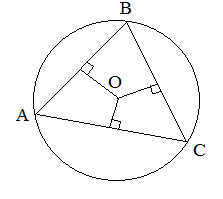
Радиус описанной окружности около треугольника

ТЕОРЕМА

Расширенная теорема синусов. Радиус $R$ окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла:

$R=\frac{AB}{2\sin \angle C} =\frac{AC}{2\sin \angle B} =\frac{BC}{2\sin \angle A}$

Примеры решения задач

ПРИМЕР 1

Задание

Найти радиус описанной окружности треугольника $ABC$ со сторонами $AB=4\sqrt{2}$ см $,\ AC=7$ см и $\angle A=45^{\circ}$ .

Решение

Радиус $R$ окружности, описанной около треугольника, равен отношению произведения сторон треугольника к его учетверенной площади:

$R=\frac{AB\cdot BC\cdot AC}{4S}$

Воспользовавшись теоремой косинусов, найдем сторону $BC$ :

$BC=\sqrt{AC^2 +AB^2 -2AC\cdot AB\cdot \cos \angle A} =$

$=\sqrt{49+32-2\cdot 7\cdot 4\sqrt{2} \cdot \frac{\sqrt{2} }2 } =\sqrt{25} =5\ cm$

Далее найдем площадь треугольника $ABC$ :

$S_{ABC} =\frac{1}{2} \cdot AB\cdot AC\cdot \sin \angle A=14\ cm^2$

Теперь можно найти радиус описанной окружности:

$R=\frac{AB\cdot BC\cdot AC}{4S} =\frac{4\sqrt{2} \cdot 5\cdot 7}{4\cdot 14} =\frac{5\sqrt{2} }{2} \ cm$

Ответ

$R=\frac{5\sqrt{2} }2$ см

ПРИМЕР 2

Задание

В треугольнике $ABC$ стороны $AB=3$ см $,\ AC=\sqrt{6}$ см. Найти все углы треугольника, если радиус описанной окружности равен $R=\sqrt{3}$ см.

Решение

Радиус описанной окружности равен отношению стороны треугольника к удвоенному синусу противолежащего угла:

$R=\frac{AB}{2\sin \angle C} =\frac{AC}{2\sin \angle B} =\frac{BC}{2\sin \angle A}$

Из данных равенств найдем синусы углов треугольника:

$\sin \angle C=\frac{AB}{2R} =\frac{3}{2\sqrt{3} } =\frac{\sqrt{3} }{2}$ , откуда $\angle C=60^{\circ}$ ,

$\sin \angle B=\frac{AC}{2R} =\frac{\sqrt{6} }{2\sqrt{3} } =\frac{\sqrt{2} }{2}$ , откуда $\angle B=45^{\circ}$ .

Найдем величину угла $A$ :

$\angle A=180^{\circ} -60^{\circ} -45^{\circ} =75^{\circ}$

Ответ

$\angle A=75^{\circ} ,\ \angle B=45^{\circ} ,\ \angle C=60^{\circ}$ .

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Радиус описанной окружности около треугольника

Определение и формула радиуса описанной окружности

Примеры решения задач