Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Стороны прямоугольного треугольника

Стороны прямоугольного треугольника

ОПРЕДЕЛЕНИЕ

Если один из углов треугольника прямой (равен ${90}^\circ$ ), то треугольник называется прямоугольным.

Стороны прямоугольного треугольника

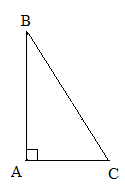
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.

Свойства сторон в прямоугольном треугольнике

Гипотенуза прямоугольного треугольника больше каждого из катетов:

$BC>AC,\ BC>AB$

Катет, лежащий против угла 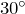$30^{\circ}$ , равен половине гипотенузы.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора):

$AC^2 +AB^2 = BC^2$

Примеры решения задач

ПРИМЕР 1

Задание

В треугольнике 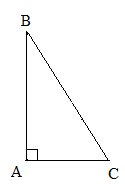$ABC$ с $\angle A=90^{\circ} ,\ \angle C=60^{\circ}$ и катетом $AB=5$ см найти длину катета $AC$ .

Решение

В прямоугольном треугольнике $ABC$ найдем угол В:

$\angle B=90^{\circ} -\angle C=90^{\circ} -60^{\circ} =30^{\circ}$

Поскольку $\angle B=30^{\circ}$ , то катет $AB$ равен половине гипотенузы $BC$ , а, значит,

$BC=2AB=10$ см

Длину катета $AC$ найдем по теореме Пифагора:

$AB=\sqrt{BC^2 -AC^2 } =\sqrt{100-25} =5\sqrt{3}$ см

Ответ

$AB=5\sqrt{3}$ см

ПРИМЕР 2

Задание

В равнобедренном прямоугольном треугольнике 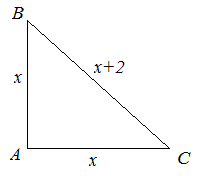$ABC$ гипотенуза больше катета на $2$ см. Найти стороны треугольника.

Решение

В треугольнике $ABC$ обозначим катеты $AB=AC=x$ , тогда $BC=2+x$ . Запишем теорему Пифагора для этого треугольника:

$BC^2 =AB^2 +AC^2 \Rightarrow (x+2)^2 =x^2 +x^2$ или $x^2 -4x-4=0$ .

Решая это уравнение и учитывая условия задачи, получим

$x=(2+2\sqrt{2} )$ см

т.е. $AB=AC=(2+2\sqrt{2} )$ см $,\ BC=(4+2\sqrt{2} )$ см.

Ответ

$AB=AC=(2+2\sqrt{2} )$ см $,\ BC=(4+2\sqrt{2} )$ см.

Читайте также:

Признаки прямоугольного треугольника

Признаки равенства треугольников

Равенство треугольников

Высота в прямоугольном треугольнике

Медиана в прямоугольном треугольнике

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook