Углы в прямоугольном треугольнике

ОПРЕДЕЛЕНИЕ

Если один из углов треугольника прямой (то есть равен ${90}^\circ$ ), то треугольник называется прямоугольным.

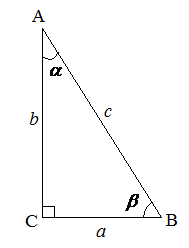
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла – гипотенузой.

Свойства углов в прямоугольном треугольнике

Сумма острых углов треугольника равна $90^{\circ}$ :

$\angle B+\angle C=90^{\circ}$

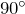Катет, лежащий против угла 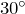$30^{\circ}$ , равен половине гипотенузы

В прямоугольном треугольнике $ABC$ с $\angle C=90^{\circ} ,\ \angle A=\alpha$ , гипотенузой $AB=c$ и катетами $AC=b$ и $BC=a$ углы определяются с помощью тригонометрических функций:

$\sin \alpha =\frac{BC}{AB} =\frac{a}{c},\ \cos \alpha =\frac{AC}{AB} =\frac{b}{c} ,\ \text{tg}\alpha =\frac{BC}{AC} =\frac{a}{b} ,\ \text{ctg}\alpha =\frac{AC}{BC} =\frac{b}{a}$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике $ABC$ с $\angle A=90^{\circ}$ , гипотенузой $BC=2\sqrt{3}$ см и катетом $AC=3$ см найти $\angle B$ и $\angle C$ .

Решение

Поскольку в прямоугольном треугольнике $ABC$ известны длины гипотенузы и катета, то можно найти

$\sin \angle B=\frac{AC}{BC} =\frac{3}{2\sqrt{3} } =\frac{\sqrt{3} }{2}$

Отсюда следует, что $\angle B=60^{\circ}$ . Тогда второй острый угол треугольника

$\angle C=90^{\circ} -\angle B=90^{\circ} -60^{\circ} =30^{\circ}$

Ответ

$\angle B=60^{\circ} ,\ \angle C=30^{\circ}$ .

ПРИМЕР 2

Задание

В прямоугольном треугольнике 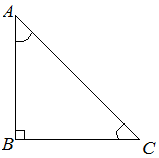$ABC\ \angle A=45^{\circ} ,\ \angle B=90^{\circ} ,\ AB=5$ см. Найти $AC$ .

Решение

Поскольку треугольник $ABC$ – прямоугольный, то

$\angle C=90^{\circ} -\angle A=90^{\circ} -45^{\circ} =45^{\circ}$

Так углы A и С равны, то $\Delta ABC$ – равнобедренный с боковыми сторонами $AB=BC=5$ см. Тогда гипотенузу $AC$ можно найти с помощью теоремы Пифагора:

$AC=\sqrt{AB^2 +BC^2 } =\sqrt{50} =5\sqrt{2}$ см

Ответ

$AC=5\sqrt{2}$ см

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Углы в прямоугольном треугольнике

Свойства углов в прямоугольном треугольнике

Примеры решения задач