Радиус описанной окружности равнобедренного треугольника

Определение и формулы описанной окружности равнобедренного треугольника

ОПРЕДЕЛЕНИЕ

Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника.

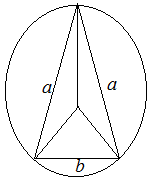
Радиус окружности, описанной около равнобедренного треугольника

Радиус описанной окружности для любого треугольника вычисляется по формуле

$R=\frac{abc}{4S} ,$

где $a,b,c$ – стороны треугольника, а $S$ – площадь треугольника.

Рассмотрим равнобедренный треугольник (то есть треугольник, у которого две стороны равны между собой). Тогда радиус окружности, описанной около такого треугольника, равен

$R=\frac{a^{2} b}{4S}$

Примеры решения задач

ПРИМЕР 1

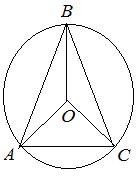
Задание

В равнобедренном треугольнике боковые стороны равны 8 см, а основание 6 см. Найти радиус окружности, описанной около этого треугольника.

Пример 1, радиус окружности, описанной около равнобедренного треугольника

Решение

Рассмотрим равнобедренный треугольник $ABC$ с боковыми сторонами $AB=BC=8$ см и основанием $AC=6$ см. Найдем полупериметр этого треугольника

$p=\frac{AB+BC+AC}{2} =\frac{8+8+6}{2} =\frac{22}{2} =11 cm$

и его площадь по формуле Герона

$S=\sqrt{p(p-AB)(p-BC)(p-AC)} =\sqrt{11\cdot 3\cdot 3\cdot 5} =3\sqrt{55} cm ^{2}$

Тогда радиус окружности, описанной около треугольника $ABC$ , равен

$R=\frac{8^{2} \cdot 6}{4\cdot 3\sqrt{55}} =\frac{32}{\sqrt{55}} =\frac{32\sqrt{55}}{55} cm$

Ответ

$R=\frac{32\sqrt{55}}{55}$ см

ПРИМЕР 2

Задание

Найти радиус окружности, описанной около равнобедренного треугольника, если его площадь равна 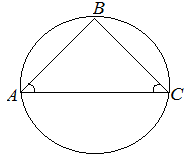$50 cm ^{2}$ , а угол при основании $45^{\circ}$ .

Пример 2, радиус окружности, описанной около равнобедренного треугольника

Решение

Рассмотрим равнобедренный треугольник $ABC$ с основанием $AC$ . Поскольку углы при основании равны $45^{\circ}$ , то

$\angle B=180^{\circ} -45^{\circ} -45^{\circ} =90^{\circ} ,$

а значит треугольник $ABC$ – прямоугольный. Тогда

$S=\frac{1}{2} \cdot AB\cdot BC=\frac{AB^{2}}{2} =50\Rightarrow AB^{2} =100,$

откуда $AB=BC=10$ см. Найдем сторону $AC$ (гипотенузу) потеореме Пифагора:

$AC=\sqrt{AB^{2} +BC^{2}} =\sqrt{100+100} =10\sqrt{2} cm$

Радиус окружности, описанной около прямоугольного треугольника $ABC$ , найдем по формуле

$R=\frac{AC}{2} =\frac{10\sqrt{2}}{2} =5\sqrt{2} cm$

Ответ

$R=5\sqrt{2}$ см

Понравился сайт? Расскажи друзьям!