Радиус описанной окружности прямоугольного треугольника

Определение и формулы описанной окружности прямоугольного треугольника

ОПРЕДЕЛЕНИЕ

Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью.

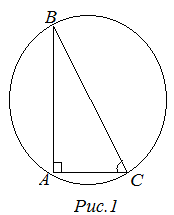
Радиус окружности описанной около прямоугольного треугольника

Окружность, описанная около треугольника, содержит все вершины треугольника. Центр описанной окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

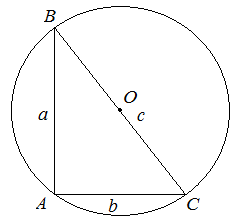
Рассмотрим прямоугольный треугольник с гипотенузой $c$ и катетами $a$ и $b$ . Центр этой окружности лежит на середине гипотенузы, а ее радиус равен половине гипотенузы

$R=\frac{c}{2}$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике с катетом 4 см и прилежащим острым углом $60^{\circ}$ найти радиус описанной окружности.

Решение

Рассмотрим прямоугольный треугольник $ABC$ ( $\angle A=90^{\circ}$ ), в котором $\angle C=60^{\circ}$ и катет $AC=4$ см. Найдем величину угла $B$ :

$\angle B=90^{\circ} -60^{\circ} =30^{\circ}$

В прямоугольном треугольнике катет, лежащий против угла $30^{\circ}$ , равен половине гипотенузы, т.е.

$AC=\frac{1}{2} BC \Rightarrow BC=2AC \Rightarrow BC=8 cm$

Теперь найдем радиус описанной окружности:

$R=\frac{1}{2} BC=4 cm$

Ответ

$R=4$ см

ПРИМЕР 2

Задание

Около прямоугольного треугольника, один из катетов которого на 7 см меньше второго, описана окружность диаметра 13 см. Найти все стороны треугольника.

Решение

Рассмотрим прямоугольный треугольник $ABC$ с $\angle A=90^{\circ}$ (рис. 1) Пусть катет $AB=x$ , тогда $AC=x-7$ . Поскольку диаметр описанной окружности равен 13 см, а гипотенуза $BC=2R=d$ , то $BC=13$ см. Запишем теорему Пифагора для рассматриваемого треугольника:

$AB^{2} +AC^{2} =BC^{2}$