Признаки прямоугольного треугольника
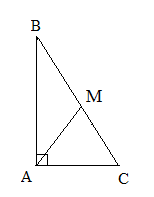
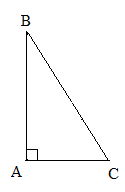
Стороны, которые образуют прямой угол, называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
Основные признаки прямоугольного треугольника
- Сумма острых углов треугольника равна
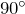 :
:
![Rendered by QuickLaTeX.com \[\angle B+\angle C=90^{\circ} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-36f397464a639e09fefb23d62ca58bc4_l3.png)
- Гипотенуза прямоугольного треугольника больше каждого из катетов:
![Rendered by QuickLaTeX.com \[BC>AC,\ BC>AB\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-92bc50810339789aae4a4dc5a4042301_l3.png)
- Катет, лежащий против угла
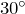 , равен половине гипотенузы.
, равен половине гипотенузы. - Две высоты прямоугольного треугольника совпадают с его катетами.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
- Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:
![Rendered by QuickLaTeX.com \[AM=R\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3e5dbcfaeacd4cfd16c422c46fcd02ed_l3.png)
- Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
![Rendered by QuickLaTeX.com \[AC^2+AB^2 = BC^2 \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6591c29ad88b7fc1bbc94eda51e76f52_l3.png)
Примеры решения задач
| Задание | В треугольнике 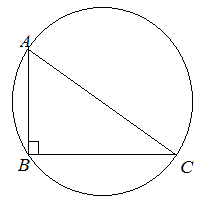
|
| Решение | Треугольник
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, следовательно, |
| Ответ |
|
| Задание | В прямоугольном треугольнике |
| Решение | В прямоугольном треугольнике катет, лежащий против угла
Найдем катет
|
| Ответ |
|











