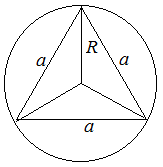
Радиус окружности, описанной около правильного треугольника

Определение и формулы окружности, описанной около правильного треугольника

ОПРЕДЕЛЕНИЕ

Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника.

Радиус описанной окружности для любого треугольника вычисляется по формуле

$R=\frac{abc}{4S} ,$

где $a,b,c$ – стороны треугольника, а $S$ – его площадь.

Рассмотрим правильный треугольник, у которого все стороны равны между собой. Тогда радиус окружности, описанной около этого треугольника, будет равен

$R=\frac{a^{3}}{4\cdot \frac{a^{2} \sqrt{3}}{4}}$

или

$R=\frac{a}{\sqrt{3}} =\frac{a\sqrt{3}}{3}$

ПРИМЕР 1

Задание

Найти радиус окружности, описанной около правильно треугольника, если его площадь равна $9\sqrt{3}$ см $^{2}$

Решение

Рассмотрим правильный треугольник со стороной a. Запишем формулу площади этого треугольника

$S=\frac{a^{2} \sqrt{3}}{4} =9\sqrt{3} ,$

откуда

$a^{2} =\frac{36\sqrt{3}}{\sqrt{3}} =36\Rightarrow a=6 cm$

Тогда радиус описанной окружности

$R=\frac{a\sqrt{3}}{3} =2\sqrt{3} cm$

Ответ

$R=2\sqrt{3}$ см

ПРИМЕР 2

Задание

Найти длину окружности, описанной около правильного треугольника со стороной 3 см.

Решение

Длина окружности вычисляется по формуле

$C=2\pi R$

Найдем радиус описанной окружности

$R=\frac{a}{\sqrt{3}} =\frac{3}{\sqrt{3}} =\sqrt{3} cm$

Тогда длина окружности будет равна

$C=2\sqrt{3} \pi \ cm$

Ответ

$C=2\sqrt{3} \pi$ см

Понравился сайт? Расскажи друзьям!