Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Окружность, вписанная в треугольник

Окружность, вписанная в треугольник

Определение и формулы окружности, вписанной в треугольник

ОПРЕДЕЛЕНИЕ

Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.

Окружность, вписанная в треугольник

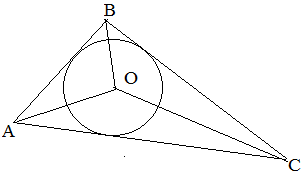
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

В любой треугольник можно вписать окружность, причем только одну.
Радиус вписанной окружности равен отношению площади треугольника к его полупериметру:

$r=\frac{S}{p}$

Примеры решения задач

ПРИМЕР 1

Задание

В треугольнике $ABC$ стороны $AB=3$ см $, BC=5$ см и $AC=6$ см. Найти радиус окружности, вписанной в треугольник $ABC$ .

Решение

Радиус вписанной окружности равен отношению площади треугольника к его полупериметру. Полупериметр треугольника $ABC$ равен

$p=\frac{1}{2} \cdot \left(AB+BC+AC\right)=\frac{1}{2} \cdot \left(3+5+6\right)=7\ cm$

Площадь треугольника найдем по формуле Герона:

$S=\sqrt{p(p-a)(p-b)(p-c)} =\sqrt{7\cdot (7-3)\cdot (7-5)\cdot (7-6)} =\sqrt{56}$ см $^{2}$

Тогда радиус вписанной окружности равен:

$r=\frac{S}{p} =\frac{\sqrt{56} }{7} =\sqrt{\frac{8}{7}}\ cm$

Ответ

ПРИМЕР 2

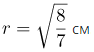Задание

В прямоугольном треугольнике $ABC$ с прямым углом $B$ катет $AB=5$ см и гипотенуза $AC=13$ см. Найти радиус окружности, вписанной в этот треугольник.

Решение

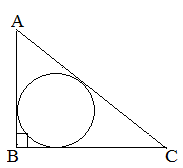
Радиус вписанной окружности равен отношению площади треугольника к его полупериметру: $r=\frac{S}{p}$ . Найдем катет $BC$ по теореме Пифагора:

$BC=\sqrt{AC^{2} -AB^{2} } =\sqrt{13^{2} -25^{2} } =12$ см

Тогда площадь прямоугольного треугольника $ABC$ равна

$S_{ABC} =\frac{1}{2} AB\cdot BC=\frac{1}{2} \cdot 5\cdot 12=30\ cm^{2}$

Полупериметр треугольника $ABC$ равен:

$p=\frac{AB+BC+AC}{2} =\frac{5+13+12}{2} =15\ cm$

Искомый радиус

$r=\frac{S}{p} =\frac{30}{15} =2\ cm$

Ответ

$r=2$ см

Читайте также:

Окружность, описанная около треугольника

Формулы треугольника

Египетский треугольник

Неравенство треугольника

Виды треугольников

Тупоугольный треугольник

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook