Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Высота в прямоугольном треугольнике

Высота в прямоугольном треугольнике

Определение и формулы высоты в прямоугольном треугольнике

ОПРЕДЕЛЕНИЕ

Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

В прямоугольном треугольнике высоты, опущенные из вершин острых углов, совпадают с катетами треугольника, а высота, опущенная из вершины прямого угла на гипотенузу, делит треугольник на два треугольника, подобных исходному и подобных друг другу.

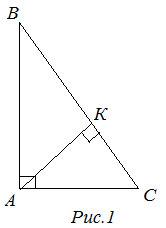
Высота в прямоугольном треугольнике

Длина высоты треугольника $ABC$ (рис.1), проведенной к гипотенузе $BC$ , находится по формуле

$AK^{2} =BK\cdot KC,$

где $BK$ и $KC$ – проекции катетов на гипотенузу.

Площадь треугольника $ABC$ можно найти по формуле

$S=\frac{1}{2} BC\cdot AK$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике $ABC$ высота $AK$ делит гипотенузу на отрезки $BK=3$ см и $KC=2$ см. Найти катеты треугольника.

Решение

Найдем квадрат длины высоты $AK$ пользуясь формулой

$AK^2 =BK\cdot KC=3\cdot 2=6$

Рассмотрим прямоугольные треугольники $AKC$ и $BKC$ , и найдем в них стороны $AC$ и $AB$ :

$AC=\sqrt{AK^2 +KC^2 } =\sqrt{6+4} =\sqrt{10}$ см

$AB=\sqrt{AK^2 +KB^2 } =\sqrt{6+9} =\sqrt{15}$ см

Ответ

$AC=\sqrt{10}$ см $,\ AB=\sqrt{15}$ см

ПРИМЕР 2

Задание

В прямоугольном треугольнике $ABC$ катеты равны $6$ см и $8$ см. Найти высоту $BK$ , опущенную на гипотенузу $AC$ .

Решение

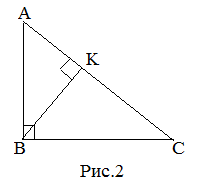
Пусть катет $AB=6$ см, а $BC=8$ см (рис. 2). Тогда по теореме Пифагора гипотенуза

$AC=\sqrt{AB^2 +BC^2 } =\sqrt{36+64} =10$ см

Площадь прямоугольного треугольника равна половине произведения катетов, т.е.

$S=\frac{1}{2} AB\cdot BC=24\ cm^2$

Высоту $BK$ найдем по формуле

$BK=\frac{2S}{AC} =\frac{2\cdot 12}{10} =2,4\ cm$

Ответ

$BK=2,4$ см

Читайте также:

Медиана в прямоугольном треугольнике

Равенство треугольников

Подобные треугольники

Соотношение между сторонами и углами треугольника

Центр окружности описанной около треугольника

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook