Свойства высоты треугольника
ОПРЕДЕЛЕНИЕ
Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение.
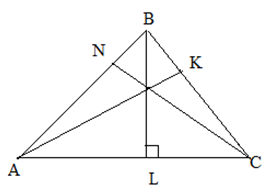
Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Свойства высоты треугольника
- В остроугольном треугольнике высоты пересекаются внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – в вершине прямого угла.
- В прямоугольном треугольнике катеты являются высотами.
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
- В равнобедренном треугольнике высота, опущенная на основание, является медианой и биссектрисой.
- В равностороннем треугольнике все высоты являются медианами и биссектрисами.
Примеры решения задач
ПРИМЕР 1
| Задание | В треугольнике 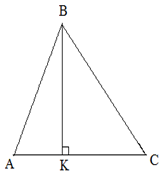
|
| Решение | В треугольнике |
| Ответ |
ПРИМЕР 2
| Задание | В прямоугольном треугольнике 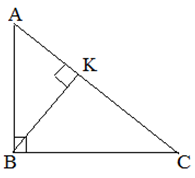
|
| Решение | Треугольники откуда Из прямоугольных треугольников Далее найдем площадь треугольника |
| Ответ |











