Подобные треугольники

Определение и формулы подобных треугольников

ОПРЕДЕЛЕНИЕ

Треугольники называются подобными, если у них равные углы и соответствующие стороны пропорциональны.

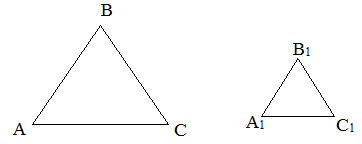
Рис.1

Например, на рисунке 1 изображены треугольники $ABC$ и $A_1 B_1 C_1$ , у которых

$\angle A=\angle A_1 ,\ \angle B=\angle B_1 ,\ \angle C=\angle C_1,\ \frac{AB}{A_1 B_1 } =\frac{BC}{B_1 C_1 } =\frac{CA}{C_1 A_1 } =2$

По определению, эти треугольники подобные. Пишут: $\Delta ABC\sim \Delta A_1 B_1 C_1$ .

Число 2, которое равняется отношению соответствующих сторон, называют коэффициентом подобия.

Если $\Delta ABC\sim \Delta A_1 B_1 C_1$ и $\Delta A_1 B_1 C_1 \sim \Delta A_2 B_2 C_2$ , то $\Delta ABC\sim \Delta A_2 B_2 C_2$ .

ЛЕММА

Лемма (Про подобные треугольники). Прямая параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от данного треугольника ему подобный.

Примеры решения задач

ПРИМЕР 1

Задание

Подобны ли треугольники $ABC$ и $MNK$ , если $\angle =40^{\circ} ,\ \angle B=82^{\circ} ,\ \angle M=40^{\circ}$ , $\angle K=58^{\circ} ,\ AB=2,4$ см $, BC=2,1$ см $,\ AC=3,9$ см $,\ MN=3,2$ см $, NK=2,8$ см $, MK=5,2$ см?

Решение

В треугольнике $ABC$ найдем угол

$\angle C=180^{\circ} -\angle A-\angle B=180^{\circ} -40^{\circ} -82^{\circ} =58^{\circ} ,$

а в треугольнике $MNK$ угол

$\angle N=180^{\circ} -\angle M-\angle K=180^{\circ} -40^{\circ} -58^{\circ} =82^{\circ} ,$

т.е. углы этих треугольником равны. Найдем отношение соответствующих сторон данных треугольников

$\frac{AB}{MN} =\frac{BC}{NK} =\frac{AC}{MK}$

или

$\frac{2,4}{3,2} =\frac{2,1}{2,8} =\frac{3,9}{5,2} =\frac{3}{4}\frac{3}{4}$

Стороны треугольников пропорциональны, следовательно, треугольники $ABC$ и $MNK$ подобны с коэффициентом подобия $\frac{3}{4}$ .

Ответ

Треугольники $ABC$ и $MNK$ Подобны.

ПРИМЕР 2

Задание

Известно, что $\Delta ABC \sim \Delta A_1 B_1 C_1$ , причем $\angle A=\angle A_1$ , $\angle B=\angle B_1, AB=6$ см $, BC=7$ см $,\ AC=10$ см $,\ A_1 B_1 =9$ см. Найти $B_1 C_1$ и $A_1 C_1$ .