Площадь прямоугольного треугольника
Для вычисления площади прямоугольного треугольника ![]() используются следующие формулы:
используются следующие формулы:

Примеры решения задач
| Задание | Один из катетов и гипотенуза прямоугольного треугольника соответственно равны 12 см и 13 см. Найти площадь треугольника. |
| Решение | Обозначим катет Подставим исходные данные в последнее равенство
Далее для вычисления площади заданного треугольника воспользуемся формулой Подставляя значения
|
| Ответ |
| Задание | В прямоугольном треугольнике один из катетов равен |
| Решение | Сделаем рисунок 2.
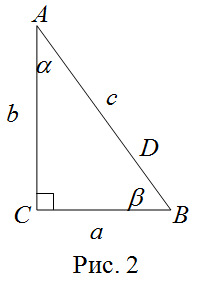
Обозначим Тогда площадь заданного треугольника будет вычисляться по формуле Подставляя в неё значения
|
| Ответ |






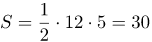 (см
(см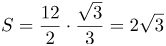 (см
(см




