Вынужденные колебания. Резонанс
Вынужденные колебания
В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной.
Вынужденные колебания в отличие от свободных могут происходить с любой частотой. Частота вынужденных колебаний совпадает с частотой внешней силы, действующей на колебательную систему. Таким образом, частота вынужденных колебаний определяется не свойствами самой системы, а частотой внешнего воздействия.
Примерами вынужденных колебаний являются колебания детских качелей, колебания иглы в швейной машине, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге и т.д.
Резонанс
Резонанс возникает из-за того, что при ![]() внешняя сила, действуя в такт со свободными колебаниями, все время имеет одинаковое направление со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. Если же внешняя сила действует «не в такт», то эта силы попеременно совершает то отрицательную, то положительную работу и вследствие этого энергия системы меняется незначительно.
внешняя сила, действуя в такт со свободными колебаниями, все время имеет одинаковое направление со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. Если же внешняя сила действует «не в такт», то эта силы попеременно совершает то отрицательную, то положительную работу и вследствие этого энергия системы меняется незначительно.
На рис.1 показана зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Видно, что эта амплитуда достигает максимума при определенном значении частоты, т.е. при ![]() , где
, где ![]() собственная частота колебательной системы. Кривые 1 и 2 отличаются величиной силы трения. При малом трении (кривая 1) резонансная кривая имеет резкий максимум, при большей силе трения (кривая 2) такого резкого максимума нет.
собственная частота колебательной системы. Кривые 1 и 2 отличаются величиной силы трения. При малом трении (кривая 1) резонансная кривая имеет резкий максимум, при большей силе трения (кривая 2) такого резкого максимума нет.
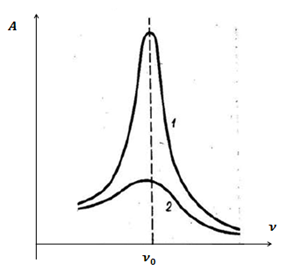
Рис.1. Резонансные кривые для различных значений силы трения.
С явлением резонанса мы часто встречаемся в повседневной жизни. Если в комнате задрожали стекла при прохождении по улице тяжелого грузовика, это значит, что собственная частота колебаний стекол равна частоте колебаний машины. Если морские волны попадают в резонанс с периодом корабля, то качка становится особенно сильной.
Явление резонанса необходимо учитывать при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены. Однако резонанс также может быть полезен. Явление резонанса используется при настройке радиоприемника на определенную частоту радиовещания, а также во многих других случаях.
Примеры решения задач
| Задание | На конец пружины горизонтального маятника, груз которого имеет массу 1 кг, действует переменная сила, частота колебаний которой равна 16 Гц. Будет ли при этом наблюдаться резонанс, если жесткость пружины 400 Н/м. |
| Решение | Определим собственную частоту колебательной системы по формуле:
Так как частота внешней силы не равна собственной частоте системы, явление резонанса наблюдаться не будет. |
| Ответ | Явление резонанса наблюдаться не будет. |
| Задание | Маленький шарик подвешен на нити длиной 1 м к потолку вагона. При какой скорости вагона шарик будет особенной сильно колебаться под действием ударов колес о стыки рельсов? Длина рельса 12,5 м. |
| Решение | Шарик совершает вынужденные колебания с частотой Если размеры шарика малы по сравнению с длиной нити, то систему можно считать математическим маятником, собственная частота колебаний которого: амплитуда вынужденных незатухающих колебаний максимальна в случае резонанса, т.е. когда откуда скорость вагона: Ускорение свободного падения Вычислим: |
| Ответ | Скорость вагона, при которой колебания шарика будут максимальны, равна 6,2 м/с. |






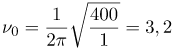 Гц
Гц




