Свободное падение. Ускорение свободного падения
Для свободно падающих тел справедлив закон Галилея: все тела под действием земного притяжения падают на Землю с одинаковым ускорением.
Ускорение свободного падения обозначается символом ![]() . Вектор ускорения свободного падения всегда направлен вертикально вниз (в общем случае — к центру Земли).
. Вектор ускорения свободного падения всегда направлен вертикально вниз (в общем случае — к центру Земли).
Ускорение свободного падения зависит от географической широты местности и неодинаково в различных точках земного шара, изменяясь примерно от ![]() м/с
м/с![]() на полюсах до
на полюсах до ![]() м/с
м/с![]() на экваторе. Ускорение свободного падения также зависит от высоты тела над поверхностью Земли: чем выше находится тело, тем меньше ускорение свободного падения. Однако, при расчетах, не требующих высокой точности, ускорение свободного падения у поверхности Земли принимают равным
на экваторе. Ускорение свободного падения также зависит от высоты тела над поверхностью Земли: чем выше находится тело, тем меньше ускорение свободного падения. Однако, при расчетах, не требующих высокой точности, ускорение свободного падения у поверхности Земли принимают равным ![]() м/с
м/с![]() .
.
Пример свободного падения и основные формулы
Простым примером свободного падения является падение тела без начальной скорости с некоторой высоты ![]() Направим координатную ось
Направим координатную ось ![]() вертикально вверх и совместим начало координат с поверхностью Земли (рис.1). Пользуясь формулами для равноускоренного движения, определим основные характеристики свободного падения:
вертикально вверх и совместим начало координат с поверхностью Земли (рис.1). Пользуясь формулами для равноускоренного движения, определим основные характеристики свободного падения:

Рис.1. Падение тела с некоторой высоты без начальной скорости
Ускорение:
![]()
Скорость:
![]()
Координата:
![]()
Из условия ![]() , можно найти время падения тела на Землю:
, можно найти время падения тела на Землю:
![Rendered by QuickLaTeX.com \[t_p=\sqrt{\frac{2h}{g}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bb89518b4f2f46dfd6961ddfb063c31a_l3.png)
Скорость тела в любой точке:
![]()
скорость тела в момент падения на Землю:
![]()
Следует также помнить о том, что свободное падение — это не всегда движение вниз. Тело, брошенное с некоторой начальной скоростью вертикально вверх, также будет двигаться равноускоренно с ускорением ![]() . При этом, так как векторы скорости и ускорения противоположно направлены, модуль скорости сначала будет уменьшаться до нуля. Потом тело, достигнув некоторой максимальной высоты, изменит направление движения и будет двигаться вниз.
. При этом, так как векторы скорости и ускорения противоположно направлены, модуль скорости сначала будет уменьшаться до нуля. Потом тело, достигнув некоторой максимальной высоты, изменит направление движения и будет двигаться вниз.
Примеры решения задач
| Задание | В последнюю секунду свободного падения тело прошло половину своего пути. С какой высоты и сколько времени падало тело? |
| Решение | Тело совершает свободное падение с начальной скоростью, равной нулю (рис.1).
При таком движении координата тела меняется со временем по закону: В момент падения тела на Землю, его координата равна нулю: Из условия откуда время падения: За 1 секунду до падения время поэтому можно записать: Подставив в последнее соотношение выражение для времени падения, находим высоту, с которой падало тело: Ускорение свободного падения Высота, с которой падало тело: Время падения тела: |
| Ответ | Тело падало с высоты 57,1 м в течение 3,4 с. |
| Задание | Два тела начинают падать с одной и той же высоты одно вслед за другим через 1 с. Через какое время, считая от начала падения первого тела, расстояние между телами будет равно 10 м? |
| Решение | Направим координатную ось как показано на рисунке.
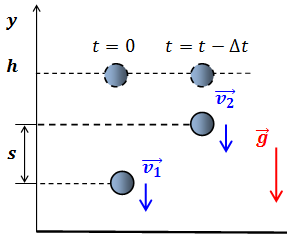
Запишем законы движения обоих тел, учитывая, что они падают без начальной скорости: Расстояние между телами в процессе падения: Таким образом, расстояние между телами: откуда время: Ускорение свободного падения Подставив в формулу численные значения физических величин, получим: |
| Ответ | Расстояние между падающими телами достигнет значения 10 м через 1,5 с. |






![Rendered by QuickLaTeX.com \[t_p=\sqrt{\frac{h}{g}}+1\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a0d8058919fc8840bbb75fd6bdc38bd0_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{\frac{2h}{g}}=\sqrt{\frac{h}{g}}+1\ \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8e67aa8e196e3c915dd4e0e862508e3e_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{\frac{h}{g}}\cdot \left(\sqrt{2}-1\right)=1\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-36308fe9b6d6ce0dccb10f918e93321b_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{\frac{h}{g}}=\frac{1}{\sqrt{2}-1}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-62db34dbeb0e15e8e1384f57e120fb40_l3.png)





