Угловая и линейная скорости

ОПРЕДЕЛЕНИЕ

Угловая скорость — это физическая величина, равная отношению угла поворота к интервалу времени, в течение которого этот поворот произошел:

$\omega =\frac{\varphi }{t}$

В системе СИ угловая скорость измеряется в рад/с.

Основные характеристики и формулы

Так как за период $T$ угловое перемещение $\varphi =2\pi$ рад, угловая скорость связана с периодом и частотой вращения:

$\omega =\frac{2\pi }{T}$

$\omega =2\pi n$

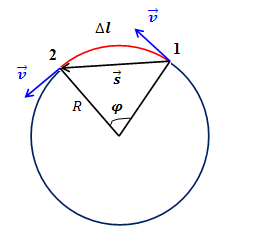
Рис.1. Линейное и угловое перемещение при равномерном движении точки по окружности

Наряду с понятием угловой скорости для характеристики равномерного движения по окружности сохраняет смысл привычное для нас понятие скорости движения точки вдоль траектории, которое в данном случае называется линейной скоростью.

Модуль линейной скорости равен отношению длины дуги окружности $\Delta l$ к промежутку времени, за который эта дуга пройдена.

Линейная скорость тела, которое движется по окружности, не изменяется по модулю, а все время изменяется по направлению, и в любой точке траектории направлена по касательной к дуге этой окружности (рис.1).

Угловая и линейная скорости связаны между собой соотношением:

$v=\omega R\$

где $R-$ радиус окружности.

Кинематическое уравнение или закон движения точки по окружности:

$\varphi ={\varphi }_0+\omega t$

Примеры решения задач

ПРИМЕР 1

Задание

К цилиндрическому валу с радиусом основания 5 м прикреплен шнур. Вал начинает равномерно вращаться, и через 5 секунд на него намоталось 20 м шнура. Чему равна угловая скорость вращения вала?

Решение

За некоторое время $t$ произвольная точка на ободе вала проходит путь, равный длине шнура, поэтому модуль линейной скорости точки:

$v=\frac{l}{t}$

Учитывая, что угловая и линейная скорости связаны между собой соотношением:

$v=\omega R$

запишем:

$\frac{l}{t}=\ \omega R\$

откуда угловая скорость вращения вала:

$\omega =\frac{l}{Rt}\$

$\omega =\frac{20}{5\cdot 5}=0,8$

Ответ

Угловая скорость вращения вала 0,8 рад/с .

ПРИМЕР 2

Задание

При увеличении в 4 раза радиуса круговой орбиты искусственного спутника земли период его обращения увеличивается в 8 раз. Во сколько раз изменяется скорость движения спутника по орбите?

Решение

Линейные скорости спутника в первом и во втором случае:

$v_1={\omega }_1R_1=\frac{2\pi }{T_1}\cdot R_1$