Равномерное движение материальной точки по окружности

ОПРЕДЕЛЕНИЕ

Равномерное движение материальной точки по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.

Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.

В окружающем нас мире мы часто сталкиваемся с подобным движением — при любом вращении твердого тела вокруг некоторой закрепленной оси все точки этого тела движутся по окружностям.

Основные характеристики и формулы

Пусть материальная точка $M$ движется по окружности радиуса $R$ (рис.1). Начало декартовой системы координат поместим в центр окружности. Тогда положение точки на окружности однозначно определяется углом поворота $\varphi$ между осью $x$ и радиус-вектором точки.

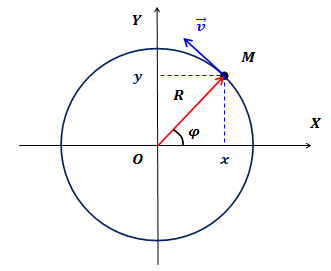
Рис.1. Равномерное движение тела по окружности

Условились положительным считать направление вращения против часовой стрелки.

Декартовые координаты точки однозначно определяются углом поворота точки:

$\left\{ \begin{array}{c} x=R\cos\varphi \\ y=R\sin\varphi \end{array} \ \right$

При движении точки по окружности ее координата, то есть угол поворота $\varphi$ , изменяется или становится функцией времени. Поэтому закон движения в этом случае — это зависимость угла поворота от времени: $\varphi =\varphi \left(t\right)$ .