Центростремительное ускорение
Основные формулы центростремительного ускорения
Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка.
Модуль центростремительного ускорения определяется формулой:
![]()
Модуль ![]() остается постоянным, однако направление вектора
остается постоянным, однако направление вектора ![]() все время меняется, поэтому движение по окружности не является равноускоренным.
все время меняется, поэтому движение по окружности не является равноускоренным.
Центростремительное ускорение также можно определить через угловую скорость:
![]()
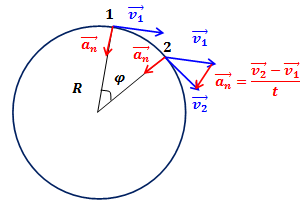
Рис.1. Центростремительное ускорение при равномерном движении точки по окружности
Примеры решения задач
| Задание | Велосипедист едет по дороге со скоростью 10 м/с. Сколько оборотов за секунду делают колеса велосипеда, если они не скользят? Какое центростремительное ускорение точки обода колеса, если его радиус 35 см? |
| Решение | Линейная скорость велосипеда связана с его угловой скоростью соотношением:
Угловая скорость: поэтому: откуда частота вращения колес: Центростремительное ускорение: |
| Ответ | Колеса велосипеда делают 4,5 оборота в секунду; центростремительное ускорение точки обода колеса 285 м/с |
| Задание | Материальная точка подвешена на нити длиной |
| Решение | Выполним рисунок.
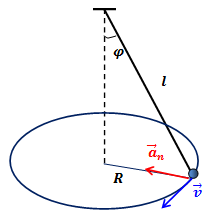
Период движения точки: Центростремительное ускорение: откуда линейная скорость точки: Подставим последнее соотношение в формулу для периода, получим: или, учитывая что |
| Ответ | Период движения точки 1,8 c. |






![Rendered by QuickLaTeX.com \[T=2\pi \sqrt{\frac{l/\\n\varphi }{a_n}}\ \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f5087dd431fd991ae9cc819b91748000_l3.png)





