Относительность движения и система отсчета в физике
Тело отсчета и система координат
Тело отсчета выбирают произвольно. Следует отметить, что движущееся тело и тело отсчета равноправны. Каждое из них при расчете движения в случае необходимости можно рассматривать или как тело отсчета, или как тело движущееся. Например, человек стоит на Земле и наблюдает, как по дороге едет автомобиль. Человек неподвижен относительно Земли и считает Землю телом отсчета, самолет и автомобиль в этом случае тела движущиеся. Однако, пассажир автомобиля, который говорит, что дорога убегает из-под колес, тоже прав. Он считает телом отсчета автомобиль (он неподвижен относительно автомобиля), Земля при этом – тело движущееся.
Чтобы фиксировать изменение положение тела в пространстве, с телом отсчета нужно связать систему координат. Система координат – это способ задания положения объекта в пространстве.
При решении физических задач наиболее распространенной является декартова прямоугольная система координат с тремя взаимно перпендикулярными прямолинейными осями – абсциссой (![]() ), ординатой (
), ординатой (![]() ) и аппликатой (
) и аппликатой (![]() ). Масштабной единицей измерения длины в СИ является метр.
). Масштабной единицей измерения длины в СИ является метр.
При ориентировании на местности пользуются полярной системой координат. По карте определяют расстояние до нужного населенного пункта. Направление движения определяют по азимуту, т.е. углу, который составляет нулевое направление с линией, соединяющей человека с нужным пунктом. Таким образом, в полярной системе координат координатами являются расстояние ![]() и угол
и угол ![]() .
.
В географии, астрономии и при расчетах движений спутников и космических кораблей положение всех тел определяется относительно центра Земли в сферической системе координат. Для определения положения точки в пространстве в сферической системе координат задают расстояние ![]() до начала отсчета и углы
до начала отсчета и углы ![]() и
и ![]() — углы, которые составляет радиус-вектор с плоскостью нулевого гринвичского меридиана (долгота) и плоскостью экватора (широта).
— углы, которые составляет радиус-вектор с плоскостью нулевого гринвичского меридиана (долгота) и плоскостью экватора (широта).
Система отсчета
Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.
При решении любой задачи о движении прежде всего должна быть указана та система отсчета, в которой будет рассматриваться движение.
При рассмотрении движения относительно подвижной системы отсчета справедлив классический закон сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной:
![]()
Примеры решения задач по теме «Относительность движения»
| Задание | Самолет движется относительно воздуха со скоростью 50 м/с. Скорость ветра относительно земли 15 м/с. Какова скорость самолета относительно земли, если он движется по ветру? против ветра? перпендикулярно направлению ветра? |
| Решение | В данном случае скорость Направим ось 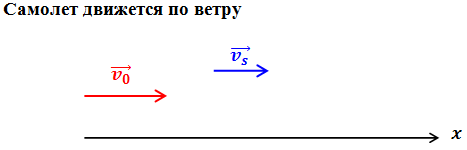
Запишем закон сложения скоростей в векторном виде: В проекции на ось Подставив в формулу численные значения, вычислим скорость самолета относительно земли:
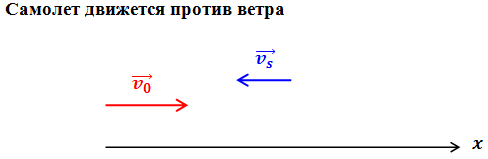
Запишем закон сложения скоростей в векторном виде: В проекции на ось Подставив в формулу численные значения, вычислим скорость самолета относительно земли:
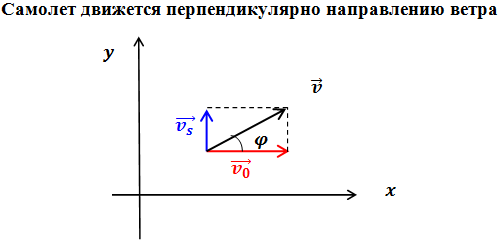
В данном случае пользуемся системой координат Складываем вектора
Эта величина представляет собой модуль вектора скорости. Для определения направления скорости самолета вычислим: Таким образом, относительно земли самолет будет двигаться со скоростью 52,2 м/с под углом |
| Ответ | Если самолет движется по ветру, то его скорость равна 65 (м/с), если против ветра, то 35 (м/с), а если перпендикулярно направлению ветра, то его скорость равна примерно 52,2 м/с. |











