Формула скорости
![Rendered by QuickLaTeX.com \[ v = \frac{S}{t} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7300d7a5cba56f21fd62049a4a9b0887_l3.png)
Здесь ![]() – скорость,
– скорость, ![]() – пройденный путь,
– пройденный путь, ![]() – время, за которое был пройден этот путь.
– время, за которое был пройден этот путь.
Единица измерения скорости – м/с (метр в секунду).
Скорость – это мера того, какое расстояние проходит тело за единицу времени. Формула верна только тогда, когда скорость не менялась на всём протяжении пути. Если происходило равноускоренное движение, то:
![]()
Где ![]() – ускорение тела,
– ускорение тела, ![]() – начальная скорость. Равноускоренное движение – такое, в котором ускорение не меняется.
– начальная скорость. Равноускоренное движение – такое, в котором ускорение не меняется.
Примеры решения задач по теме «Скорость»
| Задание | Машина за 3 часа проехала 15 км. Какова скорость машины. |
| Решение | Не забываем, что все величины нужно сначала переводить в систему СИ. Посчитаем по формуле: 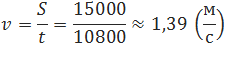
|
| Ответ | Скорость машины приблизительно равна |
| Задание | Материальная точка движется по окружности радиуса 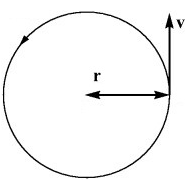
|
| Решение | Найти пройденный путь ( Намного сложнее найти перемещение (расстояние от начальной до конечной точки). Обозначим центр окружности как начало координат. Проведём радиус векторы к перемещающейся точке и точке отсчёта. Пусть угол между ними равен Очевидно, что Можно считать, что Где k – некий коэффициент пропорциональности. Найдём его из того, что нам известно. Пусть точка преодолела половину окружности. Очевидно, что её перемещение будет равно диаметру окружности, т.е. а пройдённый путь (по формуле дуги окружности): Подставим: Отсюда: |
| Ответ | 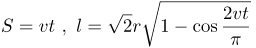 |











