Способы описания движения тела
Существует три основных способа описания механического движения: векторный, координатный и естественный. Выбор способа описания зависит от условий конкретной задачи.
Векторный способ описания движения
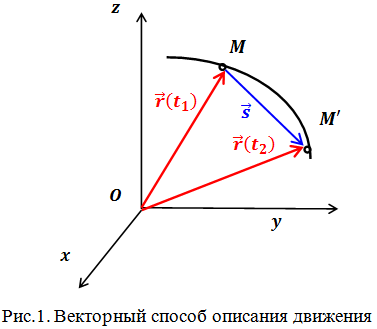
Рассмотрим движение точки ![]() в некоторой системе отсчета
в некоторой системе отсчета ![]() (рис.1). Зададим радиус-вектор точки
(рис.1). Зададим радиус-вектор точки ![]() — вектор, соединяющий начало координат с этой точкой.
— вектор, соединяющий начало координат с этой точкой.
При движении точки ![]() вектор
вектор ![]() будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость
будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость ![]() представляет собой закон движения в векторном виде.
представляет собой закон движения в векторном виде.
В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение ![]() точки.
точки.
Координатный способ описания движения
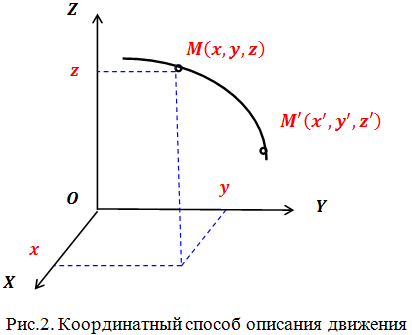
При координатном способе положение точки в пространстве задается тремя координатами (рис.2). Выбор системы координат зависит от конкретной задачи. Можно работать в декартовой (прямоугольной) системе, иногда удобнее бывает сферическая или цилиндрическая системы координат.
В декартовой системе координат положение точки определяется тройкой чисел ![]() — ее декартовыми координатами.
— ее декартовыми координатами.
Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} x=x(t) \\ y=y(t) \\ z=z(t) \end{cases} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a40db1285985e9782b17adf819cd7040_l3.png)
Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки:
![]()
Естественный способ описания движения
Пусть точка ![]() движется вдоль траектории
движется вдоль траектории ![]() в системе отсчета
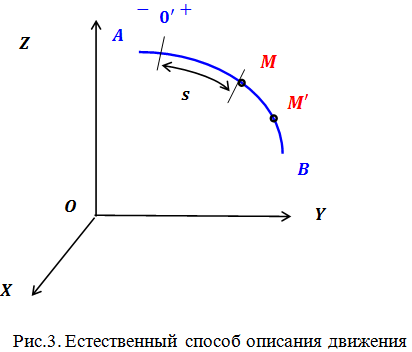
в системе отсчета ![]() (рис.3). Выберем на траектории какую-нибудь неподвижную точку
(рис.3). Выберем на траектории какую-нибудь неподвижную точку ![]() , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием
, которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием ![]() от точки
от точки ![]() . При движении точка
. При движении точка ![]() переместится в точку
переместится в точку ![]() , соответственно изменится ее расстояние от точки
, соответственно изменится ее расстояние от точки ![]() . Таким образом, расстояние
. Таким образом, расстояние ![]() зависит от времени, а характер этой зависимости позволит определить положение точки
зависит от времени, а характер этой зависимости позволит определить положение точки ![]() на траектории в любой момент времени. Закон движения в этом случае имеет вид:
на траектории в любой момент времени. Закон движения в этом случае имеет вид: ![]() .
.
Примеры решения задач по теме «Способы описания движения»
| Задание | Тело переместилось из точки |
| Решение | Сделаем чертеж
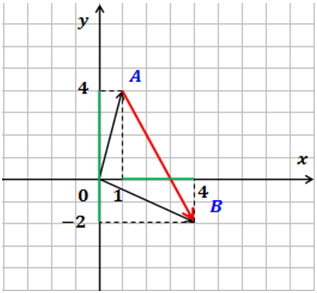
Вектор Проекции вектора перемещения на координатные оси на чертеже выделены зеленым цветом и равны Модуль вектора перемещения:
|
| Ответ | Перемещение тела равно 6,7 масштабных единиц. |
| Задание | Тело начало движение из точки |
| Решение | Сначала сделаем чертеж

Перемещение тела – вектор Модуль перемещения Расстояние, пройденное телом:
|
| Ответ | Перемещение тела равно 12 м, а расстояние равно 28 м. |











