Движение тела, брошенного под углом к горизонту

ОПРЕДЕЛЕНИЕ

Движение тела под углом к горизонту, как и движение тела, брошенного горизонтально — это сложное криволинейное движение, которое можно представить в виде суммы двух независимых движений — равномерного прямолинейного движения в горизонтальном направлении и свободного падения по вертикали.

Основные характеристики и формулы

Выберем систему координат, как показано на рис.1, и запишем законы изменения основных кинематических величин для обоих направлений.

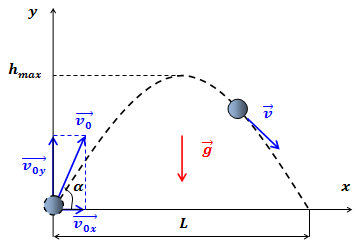
Рис.1. Движение тела, брошенного под углом к горизонту

По горизонтали (вдоль оси $x$ ):

начальное положение $x_0=0$ , начальная скорость $v_{0x}=v_0\cos\alpha$ , скорость $v_x=v_{0x}=v_0\cos\alpha ,$ ускорение $a_x=0,$ закон движения:

$x=v_0\cos\alpha t$

По вертикали (вдоль оси $y$ ):

начальное положение $y_0=0$ , начальная скорость $v_{0y}=v_0\sin\alpha$ , скорость $v_y=v_{0y}-gt=v_0\sin\alpha -gt,$ ускорение $a_y=-g,$ закон движения:

$y=v_0\sin\alpha t-\frac{gt^2}{2}$

Приведенные выше кинематические характеристики движения позволяют определить максимальную высоту подъема тела, время и дальность полета.

При достижении максимальной высоты подъема $y$ — составляющая скорости тела обращается в нуль:

$v_0\sin\alpha -gt=0$

откуда время подъема тела

$t_0=\frac{v_0\sin\alpha }{g}$

Время полета тела:

${t_p=2t}_0=\frac{{2v}_0\sin\alpha }{g}$

В верхней точке траектории $y$ — координата тела равна максимальной высоте подъема:

$h_{max}=v_0\sin\alpha t_0-\frac{g{t_0}^2}{2}=\frac{{v_0}^2{\sin}^2\alpha }{g}-\frac{{v_0}^2{\sin}^2\alpha }{2g}=\frac{{v_0}^2{\sin}^2\alpha }{2g}$

В момент падения $x$ — координата тела равна дальности полета, поэтому:

$L=v_0\cos\alpha t_p=v_0\cos\alpha \cdot \frac{{2v}_0\sin\alpha }{g}=\frac{{v_0}^2\sin2\alpha }{g}$

Траекторией движения тела, брошенного под углом к горизонту, является парабола.

Примеры решения задач

ПРИМЕР 1

Задание

Бросив камень под углом $\alpha ={45}^\circ$ к горизонту, необходимо попасть в цель, находящуюся на расстоянии $L=12$ м от места бросания и на высоте $h=2$ м. С какой скоростью необходимо бросить камень?

Решение

Направим координатные оси, как показано на рисунке.

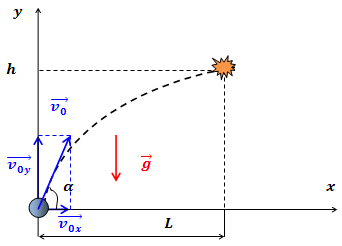
Представим сложное криволинейное движение в виде суммы независимых движений в горизонтальном и вертикальном направлениях и запишем законы изменения координат камня со временем:

$\left\{ \begin{array}{c} x=v_0\cos\alpha t \\ y=v_0\sin\alpha t-\frac{gt^2}{2} \end{array} \right.\$

В момент попадания в цель камень будет иметь координаты $\left(L,\ h\right)$ , поэтому система уравнений запишется в виде:

$\left\{ \begin{array}{c} v_0\cos\alpha t=L \\ v_0\sin\alpha t-\frac{gt^2}{2}=h \end{array} \ \ \right.\ \$

откуда, решая систему методом подстановки, будем искать начальную скорость камня $v_0.$

Выразим время из первого уравнения:

$t=\frac{L}{v_0\cos\alpha }$

и подставим это соотношение во втрое уравнение:

$v_0\sin\alpha \cdot \frac{L}{v_0\cos\alpha }-\frac{g}{2}\cdot \frac{L^2}{{\left(v_0\cos\alpha \right)}^2}=h$

$\frac{2{v_0}^2\sin\alpha \cos\alpha L-gL^2}{2{\left(v_0\cos\alpha \right)}^2}=h$

$\frac{{v_0}^2L\sin2\alpha -gL^2}{2{v_0}^2{\cos}^2\alpha }=h$

${v_0}^2L\sin2\alpha -2{v_0}^2{h\cos}^2\alpha =gL^2$

${v_0}^2\left(L\sin2\alpha -2h{\cos}^2\alpha \right)=gL^2$

$v_0=\sqrt{\frac{gL^2}{L\sin2\alpha -2h{\cos}^2\alpha }\ }$

Ускорение свободного падения $g=9,8$ м/с $^{2}$ .

Подставив в формулу численные значения физических величин, вычислим:

$v_0=\sqrt{\frac{9,8\cdot {12}^2}{12\cdot \sin{90}^\circ-2\cdot 2\cdot {\cos}^2{45}^\circ}}=12\ m/c$

Ответ

Камень необходимо бросить со скоростью 12 м/с.

ПРИМЕР 2

Задание

Под углом $\alpha ={60}^\circ$ к горизонту брошено тело с начальной скоростью 20 м/с. Через сколько времени оно будет двигаться под углом ${45}^\circ$ к горизонту?

Решение

Выберем систему координат, как показано на рисунке.

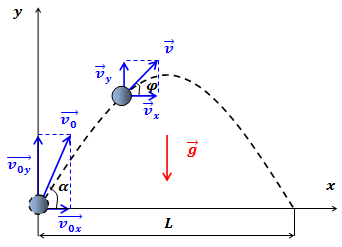
Из рисунка видно, что

$tg\varphi =\frac{v_y}{v_x}$

Запишем зависимости от времени $x$ — и $y$ — составляющих скорости тела:

${v_x=v}_0\cos\alpha$

${v_y=v}_0\sin\alpha -gt$

Подставив эти соотношения в формулу для тангенса угла, который составляет траектория полета тела с горизонтом, а также учитывая, что в данном случае $\text{tg }\varphi =\text{tg }{45}^\circ=1$ , получим: