Закон всемирного тяготения. Сила тяжести
Описание закона всемирного тяготения
Коэффициент ![]() — это гравитационная постоянная. В системе СИ гравитационная постоянная имеет значение:
— это гравитационная постоянная. В системе СИ гравитационная постоянная имеет значение:
![]()
Эта постоянная, как видно, очень мала, поэтому силы тяготения между телами, имеющими небольшие массы, тоже малы и практически не ощущаются. Однако движение космических тел полностью определяется гравитацией. Наличие всемирного тяготения или, другими словами, гравитационного взаимодействия объясняет, на чем «держатся» Земля и планеты, и почему они двигаются вокруг Солнца по определенным траекториям, а не улетают от него прочь. Закон всемирного тяготения позволяет определить многие характеристики небесных тел – массы планет, звезд, галактик и даже черных дыр. Этот закон позволяет с большой точностью рассчитать орбиты планет и создать математическую модель Вселенной.
С помощью закона всемирного тяготения также можно рассчитать космические скорости. Например, минимальная скорость, при которой тело, движущееся горизонтально над поверхностью Земли, не упадёт на неё, а будет двигаться по круговой орбите – 7,9 км/с (первая космическая скорость). Для того, чтобы покинуть Землю, т.е. преодолеть ее гравитационное притяжение, тело должно иметь скорость 11,2 км/с, (вторая космическая скорость).
Гравитация является одним из самых удивительных феноменов природы. В отсутствии сил гравитации существование Вселенной было бы невозможно, Вселенная не могла бы даже возникнуть. Гравитация ответственна за многие процессы во Вселенной – ее рождение, существование порядка вместо хаоса. Природа гравитации до сих пор до конца неразгаданна. До настоящего времени никто не смог разработать достойный механизм и модель гравитационного взаимодействия.
Сила тяжести
Частным случаем проявления гравитационных сил является сила тяжести.
![]()
Сила тяжести всегда направлена вертикально вниз (по направлению к центру Земли).
Если на тело действует сила тяжести, то тело совершает свободное падение. Вид траектории движения зависит от направления и модуля начальной скорости.
С действием силы тяжести мы сталкиваемся каждый день. Камень, брошенный в горизонтальном направлении, через некоторое время оказывается на земле. Книга, выпущенная из рук, падает вниз. Подпрыгнув, человек не улетает в открытый космос, а опускается вниз, на землю.
Рассматривая свободное падение тела вблизи поверхности Земли как результат гравитационного взаимодействия этого тела с Землей, можно записать:
![]()
откуда ускорение свободного падения:
![]()
Ускорение свободного падения не зависит от массы тела, а зависит от высоты тела над Землей. Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся около полюсов, расположены немного ближе к центру Земли. В связи с этим ускорение свободного падения зависит от широты местности: на полюсе оно немного больше, чем на экваторе и других широтах (на экваторе ![]() м/с
м/с![]() , на Северном полюсе экваторе
, на Северном полюсе экваторе ![]() м/с
м/с![]() .
.
Эта же формула позволяет найти ускорение свободного падения на поверхности любой планеты массой ![]() и радиусом
и радиусом ![]() .
.
Примеры решения задач
| Задание | Радиус Земли |
| Решение | Ускорение свободного падения у поверхности Земли:
откуда масса Земли: В системе Си радиус Земли Подставив в формулу численные значения физических величин, оценим массу Земли: |
| Ответ | Масса Земли |
| Задание | Спутник Земли движется по круговой орбите на высоте 1000 км от поверхности Земли. С какой скоростью движется спутник? За какое время спутник совершит один полный оборот вокруг Земли? |
| Решение | По второму закону Ньютона, сила, действующая на спутник со стороны Земли, равна произведению массы спутника на ускорение, с которым он движется:
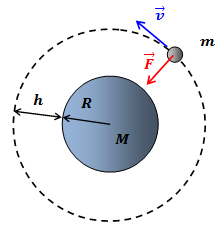
Со стороны земли на спутник действует сила гравитационного притяжения, которая по закону всемирного тяготения равна: где Так как спутник находится на некоторой высоте где Таким образом, сила гравитационного притяжения в данном случае: Подставив значение гравитационной силы в формулу для второго закона Ньютона и учитывая, что ускорение спутника – это центростремительное ускорение (спутник движется по круговой орбите), получим: или откуда скорость спутника: Время, за которое спутник совершит один полный оборот вокруг Земли, — это период его обращения по круговой орбите, который равен: |
| Ответ | Спутник движется со скоростью 7,4 км/с; один полный оборот вокруг Земли спутник совершит за 1,8 ч. |






![Rendered by QuickLaTeX.com \[M=\frac{9,8\cdot {\left(6,4\cdot {10}^6\right)}^2}{6,7\cdot {10}^{-11}}=6\cdot {10}^{24}\ kg\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a887d5989f4a03d5b25a5167c01ca7a5_l3.png)
![Rendered by QuickLaTeX.com \[v=\sqrt{\frac{6,7\cdot {10}^{-11}\cdot 6\cdot {10}^{24}}{6,4\cdot {10}^6+{10}^6}}=7,4\cdot {10}^3\ {m}/{c}=7,4\ {km}/{c}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-983b89f97fad6f38c39e932feef8c932_l3.png)





