Равноускоренное движение

Равноускоренное прямолинейное движение

ОПРЕДЕЛЕНИЕ

Равноускоренное прямолинейное движение — это такое движение, при котором скорость тела за равные промежутки времени изменяется одинаково, другими словами, это движение с постоянным ускорением.

Траектория движения в данном случае — прямая линия.

Основные формулы и кинематические характеристики

Ускорение $\overline{a}=const$ (по модулю и по направлению).

Скорость тела меняется по закону

$\overline{v}={\overline{v}}_0+\overline{a}t$

где ${\overline{v}}_0-$ начальная скорость движения.

Закон движения в случае равноускоренного движения имеет вид:

$\overline{r}={\overline{r}}_0+{\overline{v}}_0t+\frac{\overline{a}t^2}{2}\$

где $\overline{r}-$ радиус-вектор точки в момент времени $t$ , $\overline{r}_0-$ радиус-вектор начального положения точки, ${\overline{v}}_0-$ начальная скорость, $\overline{a}-$ ускорение.

В одномерном случае закон движения запишется в виде:

$x=x_0+v_{0x}t+\frac{a_xt^2}{2}\$

Для двумерного случая (движения по плоскости) закон движения в случае равноускоренного движения запишется в виде системы двух уравнений:

$\left\{ \begin{array}{c} x=x_0+v_{0x}t+\frac{a_xt^2}{2} \\ y=y+v_{0y}t+\frac{a_yt^2}{2} \end{array} \right.$

Также справедлива так называемая формула для определения пути «без времени»:

$s=\frac{v^2-{v_0}^2}{2a}\ .$

Графическое изображение зависимости кинематических характеристик от времени представлено на рисунках 1-3.

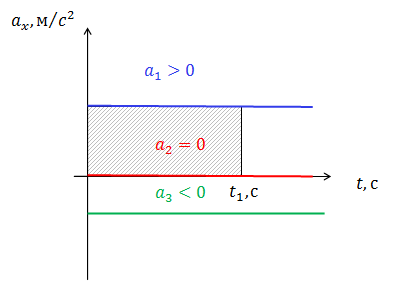
Рис.1. Зависимость ускорения от времени при равноускоренном движении

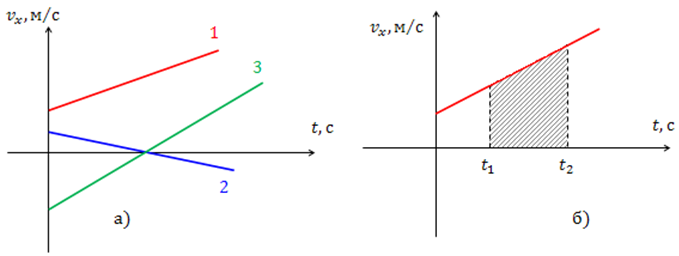
Рис.2. Зависимость скорости от времени при равноускоренном движении: а) закон изменения скорости для различных случаев; б) определение перемещения с помощью графика скорости.

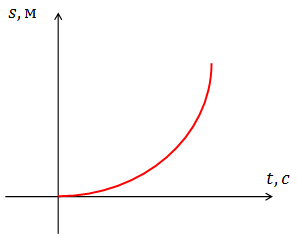
Рис.3. Зависимость перемещения от времени при равноускоренном движении.

На рис.1 изображен график зависимости ускорения от времени при равноускоренном движении. Случай $a>0$ соответствует равноускоренному движению, случай $a<0$ — равнозамедленному движению, случай $a=0$ — равномерному движению. Площадь заштрихованного прямоугольника численно равна средней скорости движения тела.

На рис.2 представлена зависимость скорости от времени при равноускоренном движении. Рис.2 (а) демонстрирует разные случаи движения: 1- тело двигалось в направлении оси $x$ равноускоренно; 2 — тело двигалось равнозамедленно в направлении оси $x$ , затем остановилось и поменяло направление движения; 3- тело двигалось равноускоренно в направлении, противоположном оси $x$ , затем остановилось и стало двигаться в противоположном направлении. Во всех трех случаях тело имело начальные скорости.

По графику скорости можно определить ускорение движущегося объекта как тангенс угла наклона прямой зависимости $a(t)$ к оси $x.$

Площадь заштрихованной трапеции (рис.2 (б)) численно равна пути, пройденному телом за время $\Delta t=t_2-t_1\ .$

Зависимость перемещения от времени при равноускоренном движении — это квадратичная функция (рис.3). Положение вершины параболы зависит от направлений начальной скорости и ускорения.

Примеры решения задач

ПРИМЕР 1

Задание

По графику зависимости 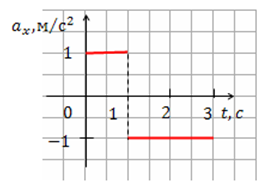$a_x(t)$ , изображенному на рисунке, построить график зависимости $v_x(t)$ , считая, что в начальный момент времени $(t=0)$ скорость движения материальной точки равна нулю.

Решение

При равноускоренном движении скорость 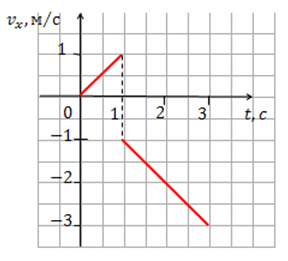$v_x$ материальной точки изменяется по закону:

$v_x\left(t\right)=v_{0x}+a_xt\$

Так как по условию задачи $v_{0x}=0$ , можно переписать:

$v_x\left(t\right)=v_{0x}+a_xt\$

На первом участке $0\le t<1$ ускорение $a_x=1$ м/с $^{2}$ , $v_x\left(t\right)=t.$ На втором участке $1\le t<3$ ускорение $a_x=-1$ м/с $^{2}$ , $v_x\left(t\right)=-t.$ График скорости имеет вид:

ПРИМЕР 2

Задание

На шоссе с одного старта с интервалом в 2 с начали движение сначала велосипедист, а затем мотоциклист. После старта велосипедист двигался равномерно со скоростью 32 км/ч, а мотоциклист — равноускоренно с ускорением 2,5 м/с $^{2}$ . Определить скорость мотоциклиста в тот момент, когда он достиг велосипедиста.

Решение

1) Аналитический способ.

Считаем шоссе прямолинейным. Запишем уравнение движения велосипедиста. Так как велосипедист двигался равномерно, то его уравнение движения:

$x_1\left(t\right)=v_1t$

(начало координат помещаем в точку старта, поэтому начальная координата велосипедиста равна нулю).

Мотоциклист двигался равноускоренно. Он также начал движение с места старта, поэтому его начальная координата равна нулю, начальная скорость мотоциклиста также равна нулю (мотоциклист начал двигаться из состояния покоя).

Учитывая, что мотоциклист начал движение на $\Delta t$ позже, уравнение движения мотоциклиста:

$x_2=\frac{a{\left(t-\Delta t\right)}^2}{2}$

При этом скорость мотоциклиста изменялась по закону:

$v_2\left(t\right)=at$

В момент, когда мотоциклист догнал велосипедиста их координаты равны, т.е. $x_1=x_2$ или:

$v_1t=\frac{a{\left(t-\Delta t\right)}^2}{2}\$

Решая это уравнение относительно $t$ , находим время встречи:

${\left(t-\Delta t\right)}^2=\frac{2v_1}{a}t;$

$t^2-2\Delta t\cdot t+\Delta t^2-\frac{2v_1}{a}t=0;$

$t^2-2\left(\frac{v_1}{a}+\Delta t\right)t+\Delta t^2=0;$

Это квадратное уравнение. Определяем дискриминант:

$D=4{\left(\frac{v_1}{a}+\Delta t\right)}^2-4\Delta t^2=4\frac{{v_1}^2}{a^2}+8\frac{v_1\Delta t}{a}+4\Delta t^2-4\Delta t^2=4\frac{v_1}{a}\left(\frac{v_1}{a}+2\Delta t\right);$

Определяем корни:

$t_1=\frac{2\left(\frac{v_1}{a}+\Delta t\right)+2\sqrt{\frac{v_1}{a}\left(\frac{v_1}{a}+2\Delta t\right)}}{2}=\frac{v_1}{a}+\Delta t+\sqrt{\frac{v_1}{a}\left(\frac{v_1}{a}+2\Delta t\right)};$

$t_2=\frac{v_1}{a}+\Delta t-\sqrt{\frac{v_1}{a}\left(\frac{v_1}{a}+2\Delta t\right)};$

Подставим в формулы числовые значения и вычислим:

$t_1=\frac{8,9}{2,5}+2+\sqrt{\frac{8,9}{2,5}\left(\frac{8,9}{2,5}+2\cdot 2\right)}=10,75 c$

$t_2=\frac{8,9}{2,5}+2-\sqrt{\frac{8,9}{2,5}\left(\frac{8,9}{2,5}+2\cdot 2\right)}=0,37 c$

Второй корень отбрасываем как несоответствующий физическим условиям задачи: мотоциклист не мог догнать велосипедиста через 0,37 с после начала движения велосипедиста, так как сам покинул точку старта только через 2 с после того, как стартовал велосипедист.

Таким образом, время, когда мотоциклист догнал велосипедиста:

$t_m=10,75 c$

Подставим это значение времени в формулу закона изменения скорости мотоциклиста и найдем значение его скорости в этот момент:

$v_2\left(t_m\right)=v_2\left(10,75\right)=2,5\cdot 10,75=26,9\ m/c$

2) Графический способ.

На одной координатной плоскости строим графики изменения со временем координат велосипедиста и мотоциклиста (график для координаты велосипедиста — красным цветом, для мотоциклиста — зеленым). Видно, что зависимость координаты от времени для велосипедиста — линейная функция, и график этой функции — прямая (случай равномерного прямолинейного движения). Мотоциклист двигался равноускоренно, поэтому зависимость координаты мотоциклиста от времени — квадратичная функция, графиком которой является парабола.

Координата времени для точки пересечения графика — это и есть время встречи велосипедиста и мотоциклиста $t_m.$

Графики зависимости от времени координат велосипедиста и мотоциклиста: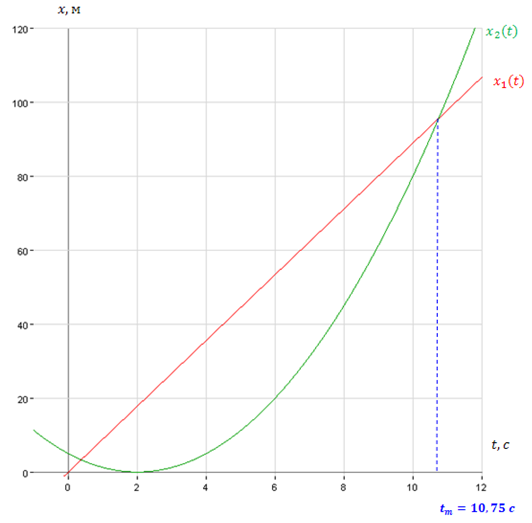

Далее строим график зависимости скорости мотоциклиста от времени $v_2(t)$ . На оси времени (горизонтальная ось) находим отметку $t_m=10,75\ c$ , строим перпендикуляр до пересечения с графиком (синий пунктир), и из этой точки опускаем перпендикуляр на вертикальную ось (синий пунктир). Точка пересечения этого перпендикуляра с вертикальной осью и даст нам значение скорости в момент времени $t_m,$ т.е. в момент, когда мотоциклист догнал велосипедиста.

График зависимости от времени скорости мотоциклиста: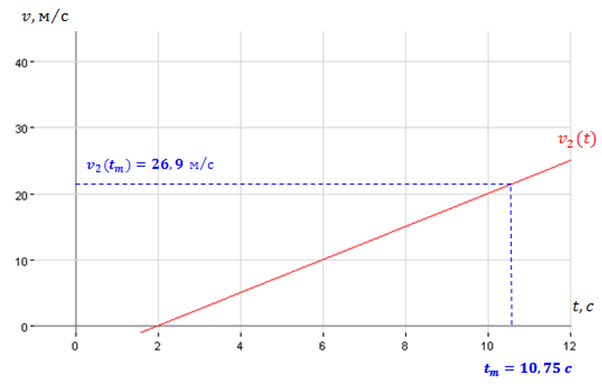

Ответ

Скорость мотоциклиста в тот момент, когда он достиг велосипедиста будет $26,9$ м/с.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Равноускоренное движение

Равноускоренное прямолинейное движение

Основные формулы и кинематические характеристики

Примеры решения задач