Движение тела, брошенного горизонтально

ОПРЕДЕЛЕНИЕ

Движение тела, брошенного горизонтально — это сложное движение по криволинейной траектории, которое можно представить как сумму двух независимых друг от друга движений — равномерного прямолинейного движения по горизонтали и свободного падения по вертикали.

Основные характеристики и формулы

Для кинематического описания движения выберем систему координат, как показано на рис.1, и запишем законы изменения кинематических характеристик движения тела для каждого из направлений.

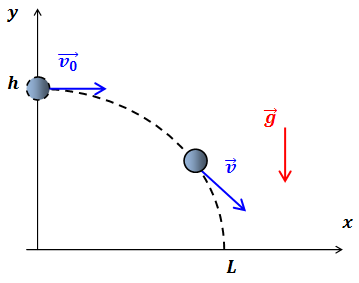
Рис.1. Движение тела, брошенного горизонтально

По горизонтали (вдоль оси $x$ ):

начальное положение $x_0=0$ , начальная скорость $v_{0x}=v_0$ , скорость $v_x=v_0,$ ускорение $a_x=0,$ закон движения:

$x=v_0t$

По вертикали (вдоль оси $y$ ):

начальное положение $y_0=h$ , начальная скорость $v_{0y}=0$ , скорость $v_y=-gt,$ ускорение $a_y=-g,$ закон движения:

$y=h-\frac{gt^2}{2}$

Используя приведенные выше законы движения, можно найти время и дальность полета тела.

В точке падения $y$ — координата тела равна нулю, поэтому можно записать:

$h-\frac{gt^2}{2}=0$

откуда время полета:

$t_p=\sqrt{\frac{2h}{g}}$

$x$ — координата тела в точке падения равна дальности полета и является расстоянием, пройденным телом вдоль оси $x$ за время $t_p$ :

$L=v_0t_p=v_0\sqrt{\frac{2h}{g}}$

Знание законов изменения координат тела с течением времени позволяет рассчитать траекторию тела. Выразив время из закона движения вдоль горизонтального направления:

$t=\frac{x}{v_0}\$

подставим это выражение в закон движения вдоль вертикального направления и получим уравнение траектории тела:

$y=h-\frac{g}{2{v_0}^2}\cdot x^2$

Полученное уравнение траектории показывает, что тело, брошенное горизонтально, двигается по параболе, вершина которой находится в точке бросания.

Примеры решения задач

ПРИМЕР 1

Задание

Камень бросили горизонтально с некоторой высоты. Через $t=2\ c$ его скорость оказалась направлена под углом $\alpha ={55}^\circ$ к горизонту. Чему равна начальная скорость камня.

Решение

Выберем систему координат, как показано на рисунке.

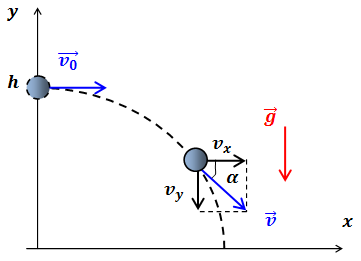
Представим сложное криволинейное движение в виде суммы независимых движений в горизонтальном и вертикальном направлениях и запишем законы изменения со временем горизонтальной и вертикальной компонент вектора скорости:

$v_x=v_0$ (горизонтальная составляющая вектора скорости не зависит от времени);

$v_y=-gt$

Скорость тела:

$v=\sqrt{{v_x}^2+{v_y}^2}=\sqrt{{v_0}^2+g^2t^2}$

Горизонтальная составляющая вектора скорости — это проекция вектора скорости на ось $x$ , поэтому:

$v_x=v\cos\alpha$

или

$v=\frac{v_0}{\cos\alpha }$

Приравнивая правые части соотношений для скорости тела, получим:

$\frac{v_0}{\cos\alpha }=\sqrt{{v_0}^2+g^2t^2}$

$\frac{{v_0}^2}{{\cos}^2\alpha }={v_0}^2+g^2t^2$

${v_0}^2\left(\frac{1}{{\cos}^2\alpha }-1\right)=g^2t^2$

Воспользуемся тригонометрической формулой:

$\frac{1}{{\cos}^2\alpha }=1+\text{tg} ^2\alpha$

получим:

${v_0}^2\left(1+\text{tg}^2\alpha -1\right)=g^2t^2$

откуда начальная скорость тела:

$v_0=\frac{gt}{\text{tg }\alpha }$

Ускорение свободного падения $g=9,8$ м/с $^{2}$ .

Подставив в формулу численные значения физических величин, получим:

$v_0=\frac{9,8\cdot 2}{\text{tg }{55}^\circ}=14 m/c$

Ответ

Начальная скорость камня 14 м/с.

ПРИМЕР 2

Задание

Из двух пунктов отвесного берега. находящихся на некоторой высоте от поверхности воды, одновременно бросают в горизонтальном направлении два тела. Начальные скорости тел 5 и 7,5 м/с . Оба тела падают в воду одновременно. Расстояние от берега до точки падения первого тела в воду 10 м. Определить: 1) продолжительность полета тел; 2) высоту, с которой они были брошены; 3) место падения второго тела в воду.

Решение

Выберем систему координат, как показано на рисунке.

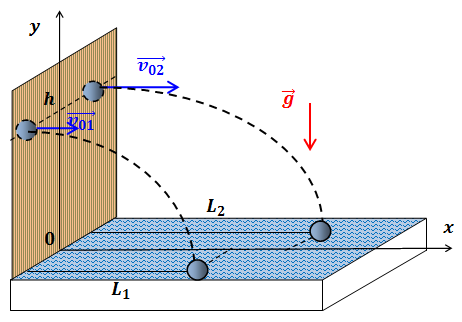
Запишем законы движения для обоих тел:

первое тело

$\left\{ \begin{array}{c} x_1=v_{01}t \\ y_1=h-\frac{gt^2}{2} \end{array} \right$

второе тело

$\left\{ \begin{array}{c} x_2=v_{02}t \\ y_2=h-\frac{gt^2}{2} \end{array} \right.\ \$

По условию задачи первое тело упало в воду на расстоянии $L_1,$ поэтому продолжительность полета первого тела также, как и второго тела 9по условию они равны) можно найти из соотношения: