Формула пути
![Rendered by QuickLaTeX.com \[ S = \frac{a t^{2}}{2} + v_{0} t \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2ba58e970b2d4fe4413390ef2b43ed44_l3.png)
Здесь ![]() – пройденный путь,
– пройденный путь, ![]() – ускорение тела,
– ускорение тела, ![]() – начальная скорость тела,
– начальная скорость тела, ![]() — время ускоренного движения.
— время ускоренного движения.
Единица измерения пути – м (метр).
Путь – скалярная величина. Путь – это мера того, какое расстояние преодолело тело в ходе движения. ![]() – это скорость, с которой тело двигалось к моменту начала ускорения. У этой формулы есть 2 частных случая:
– это скорость, с которой тело двигалось к моменту начала ускорения. У этой формулы есть 2 частных случая:
1) Движение равномерное (без ускорения)
![]()
Это самый распространённый в задачах, простейший случай. Когда про ускорение ничего не сказано, то под формулой пути имеется в виду именно эта формула.
2) Движение, начатое с неподвижного состояния (без начальной скорости)
![Rendered by QuickLaTeX.com \[ S = \frac{a t^{2}}{2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fbedb2f21229a14c560da0a208f0529a_l3.png)
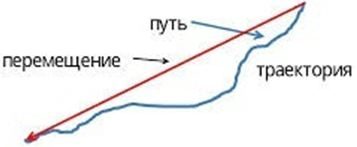
Путь не нужно путать с перемещением – мерой расстояния между конечной и начальной точкой движения.
Примеры решения задач по теме «Путь тела»
| Задание | Найти путь, который прошло тело, движущееся с ускорением 1 м/с |
| Решение | Все исходные данные нам известны. Подставим их в формулу:
|
| Ответ | Тело прошло 608 метров. |
| Задание | В первый промежуток времени тело двигалось равномерно со скоростью vв течение времени |
| Решение | Пусть Затем тело замедлялось, пока его скорость не обнулилась ( Пусть Затем тело прошло расстояние Теперь можно найти ответ: |
| Ответ |






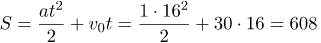 (м)
(м)![Rendered by QuickLaTeX.com \[ S_{1} + S_{2} = \frac{a t_{2}^{2}}{2} = v t + \frac{v^{2}}{2a} \text{ } \rightarrow \text{ } t_{2} = \sqrt{\frac{2 \left( v t + \frac{v^{2}}{2a} \right)}{a}} = \sqrt{\frac{2 vt}{a} + \left( \frac{v}{a} \right)^{2}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-908f33ebdbef4cead1b1ae718bdad5db_l3.png)





