Ускорение

ОПРЕДЕЛЕНИЕ

Ускорение – это физическая величина, численно равная изменению скорости за единицу времени:

$\overline{a} = \frac{\Delta \overline{v}}{t}$

Важно помнить, что ускорение – величина векторная. Говорить об ускорении можно, когда скорость изменяется как по величине, так и по направлению.

Единицей измерения ускорения в системе СИ является м/с $^{2}$ .

Примеры ускоренного движения – разгон, торможение, падение, различные маневры.

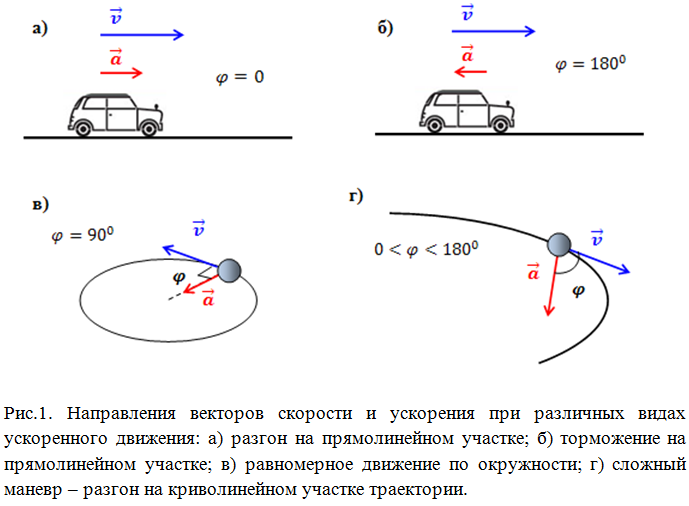
Если скорость всегда направлена по касательной к траектории движения, и направление вектора скорости совпадает с направлением движения, то вектор ускорения в общем случае может составлять любой угол с вектором скорости. Так, при разгоне по прямолинейному участку пути направления векторов скорости и ускорения совпадают (угол между векторами скорости и ускорения $0^\circ$ ) (рис.1,а). При торможении на прямолинейном участке шоссе вектора скорости и ускорения противоположно направлены (угол между векторами скорости и ускорения $180^\circ$ ) (рис.1,б).

При равномерном движении по окружности вектор ускорения перпендикулярен вектору скорости (угол между векторами скорости и ускорения $90^\circ$ ) (рис.1,в). В более общем сложном случае движения по криволинейной траектории угол между векторами скорости и ускорения зависит от кривизны траектории и интенсивности разгона/торможения, т.е. может принимать любое значение (рис.1,г).

Ускорение может быть как положительным, так и отрицательным. Если $a>0$ , говорят об ускоренном движении, если $a<0$ , движение замедленное.

Примеры решения задач по теме «Ускорение»

ПРИМЕР 1

Задание

На рисунке показан вектор ускорения 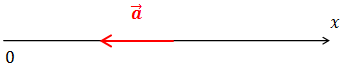$\overline{a}$ . Каков характер движения, если точка движется вправо? влево?

Ответ

1) Если точка движется вправо, вектор ее скорости будет направлен по оси $x$ . Так как вектор скорости и вектор ускорения в этом случае противоположно направлены, движение будет замедленным.

2) Если точка движется влево, направление ее скорости совпадает с направлением вектора ускорения, и движение в этом случае будет ускоренным.

ПРИМЕР 2

Задание

Шарик движется по желобу с ускорением 10 м/с $^{2}$ . Определить проекции ускорения на вертикальную и горизонтальную оси, если угол наклона желоба к горизонту $14^\circ$ .

Решение

Выберем систему координат, как показано на рисунке.

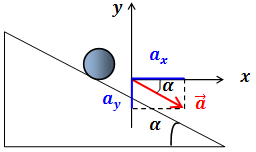
Проекция ускорения на горизонтальную ось:

$a_{x} = a \cos \alpha$

Проекция ускорения на вертикальную ось:

$a_{y} = -a \sin \alpha$

В системе СИ ускорение измеряется в м/с $^{2}$ , переводим значение ускорения в систему СИ:

$a=10$ см/с $^{2}$ $=0,1$ м/с $^{2}$

$a_{x} = 0,1 \cdot \cos 14^\circ = 0,097$ м/с $^{2}$

$a_{y} = -0,1 \cdot \sin 14^\circ = -0,024$ м/с $^{2}$

Ответ

$a_{x} = 0,097$ м/с $^{2}$ , $a_{y} = -0,024$ м/с $^{2}$

ПРИМЕР 3

Задание

Самолет при посадке коснулся посадочной полосы аэродрома при скорости 70 м/с. Через 20 с он остановился. Определить ускорение самолета при таком движении. Начертить график ускорения.

Решение

Скорость самолета в момент касания посадочной полосы $v_1=70$ м/с , конечная скорость самолета $v_2=0$ (самолет остановился).

Ускорение самолета:

$a = \frac{\Delta v}{t} = \frac{v_{2}-v_{1}}{t}$

Знаки векторов в формуле опускаем, так как рассматриваем проекцию ускорения на ось $x$ , направленную вдоль посадочной полосы по направлению движения самолета.

м/с $^{2}$

График ускорения: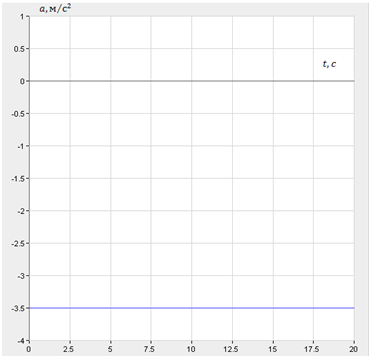

Ответ

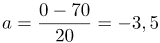$a=-3,5$ м/с $^{2}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Ускорение

Примеры решения задач по теме «Ускорение»