Скорость волны. Длина волны

Скорость волны

ОПРЕДЕЛЕНИЕ

Скорость распространения волны $v$ — это скорость распространения волнового фронта.

Скорость распространения волны зависит от типа волны (продольная или поперечная) и от свойств среды (плотности и температуры), в которой распространяется волна.

Длина волны

ОПРЕДЕЛЕНИЕ

Длина волны – это расстояние, которое проходит волновой фронт за время, равное периоду колебаний:

$\lambda =vT$

Так как частота волны

$\nu =\frac{1}{T}\$

можно получить формулу связи длины волны и частоты:

$\lambda =\frac{v}{\nu }\$

Очевидно, что поскольку скорость распространения волны зависит от свойств среды, длина волны при одинаковой частоте будет меняться при переходе волны из одной среды в другую.

На рис.1 представлена геометрическая интерпретация длины волны. Исходя из геометрической интерпретации, можно утверждать, что длина волны равна наименьшему расстоянию между точками, которые колеблются в одинаковой фазе.

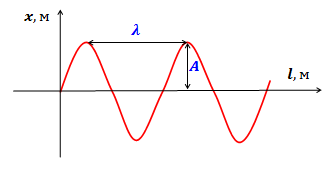
Рис.1. Геометрическая интерпретация длины волны (здесь x-смещение колеблющихся точек; $l$ — расстояние, на которое распространяется волновой фронт; $\lambda$ — длина волны; $A$ — амплитуда колебаний)

Таким образом, бегущая синусоидальная волна периодична как во времени, так и пространстве. Временной период равен периоду колебаний $T$ частиц среды, пространственный период равен длине волны $\lambda$ . Волновое число $k=\frac{2\pi }{\lambda }$ является пространственным аналогом циклической частоты $\omega =\frac{2\pi }{T}$ .

Примеры решения задач

ПРИМЕР 1

Задание

Волна цунами может иметь скорость до 100 км/ч. Определить период колебаний, если длина волны 50 км.

Решение

Длина волны определяется по формуле:

$\lambda =vT$

откуда период колебаний:

$T=\frac{\lambda }{v}\$

Переведем единицы в систему СИ: скорость волны $v=100$ км/ч $=27,8$ м/с; длина волны $\lambda =50$ км $=50000$ м.

Вычислим:

$T=\frac{50000}{27,8}=1799\ c=0,5\ hour$

Ответ

Период колебаний 0,5 ч.

ПРИМЕР 2

Задание

Волны распространяются со скоростью 360 м/с при частоте, равной 450 Гц. Чему равна разность фаз двух точек, отстоящих друг от друга на 20 см?

Решение

Разность фаз двух точек, отстоящих друг от друга на расстояние, равное длине волны, равна $2\pi$ . Если точки находятся на расстоянии $l$ друг от друга, их разность фаз:

$\Delta \varphi =\frac{l}{\lambda }\cdot 2\pi$